距離の観点からノードの分散表現を俯瞰する

こんにちは、Sansan DSOC 研究開発部の保坂です。今回の記事は、弊社のアドベントカレンダーで書いた記事で行った分析を少し丁寧にやり直してまとめたものです。

はじめに
分散表現間の距離
RPD とタスクにおける性能差との関係
RPD で計算された単語の分散表現間の関係
ノードの分散表現の学習アルゴリズム
[実験] RPD でノードの分散表現間の関係を計算してみる
[実験] RPD とノード分類タスクにおける性能との関係を調査する
さいごに

はじめに

最近では、ニュース記事などの言語データや、SNS上の友人関係のようなグラフデータを取り扱う研究がさかんになっています。これらのデータを対象にした研究がさかんになっている理由の一つとして、本来数値として扱いづらい単語やノードを、その性質を保持したベクトルとして表現する分散表現と呼ばれる技術の発達があります。

しかし、実際は多様な分散表現の学習アルゴリズムが提案されており、タスクを解く際にどのアルゴリズムを使えばいいのか迷ってしまいます。今回は様々な分散表現の学習アルゴリズムへの理解を深めるために、距離の観点から分散表現の学習アルゴリズムを俯瞰していきたいと思います。

分散表現間の距離

自然言語処理に関する研究のトップカンファレンスである ACL 2020 で、RPD: A Distance Function Between Word Embeddings という題目の発表がありました。

この研究では、異なるアルゴリズムで学習された分散表現間の距離関数として Relative pairwise inner Product Distance (RPD) を提案し、距離関数としての妥当性および単語の分散表現間の関係性について分析を行っています。

Relative pairwise inner Product Distance
あるアルゴリズムによって学習された単語の分散表現を $E$ で表現します。 $E$ は、 $i$ 行目が単語 $w_i$ の意味ベクトルを表している行列です。二つの異なる分散表現の学習アルゴリズム $E_1$ , $E_2$ 間の距離関数 RPD を以下の式で定義します。

$\displaystyle RPD(E_1, E_2) = \frac{\|\tilde{E}_1\tilde{E}_1^{\top} - \tilde{E}_2\tilde{E}_2^{\top}\|}{\|\tilde{E}_1\tilde{E}_1^{\top}\|\|\tilde{E}_2\tilde{E}_2^{\top}\|}\tag{1}$

ただし、 $\tilde{E}$ は単語の意味ベクトルの各次元の値をその標準偏差で除した値であり、 $\|\cdot\|$ はフロベニウスノルムです。

上述した RPD は以下に示すようないくつかの性質を持った関数です。各性質の証明は論文に記述されていますので、そちらを参照してみてください。

単語の意味ベクトルの各要素が標準正規分布 $\mathcal{N}(0, 1)$ に従うとき、語彙数 $V$ を $V \to \infty$ とした場合に RPD の上限は $1$ に収束する。つまり、多くの語彙を持つコーパスを用いて学習した分散表現では、分散表現間の構造が類似しているほど RPD は $0$ に近づき、類似していないほど $1$ に近い値をとる。
上記と同様に各要素が標準正規分布に従い、かつ $E_1$ と $E_2$ が独立である場合、 $RPD(E_1, E_2)$ は正規分布に従う。この性質を利用することで、二つの分散表現 $E_1$ , $E_2$ の独立性の検定を行うことが可能になる。

RPD とタスクにおける性能差との関係

論文では、RPD の妥当性を示すために、様々なアルゴリズムで学習された単語の分散表現のペアに対して、word similarity task *1 と word analogy task *2 に適用した際の性能の差と RPD の関係を調査しています。
論文中で用いられている単語の分散表現の学習アルゴリズムを以下の表に示します。

学習アルゴリズム	概要
SGNS( $k$ )	negative sample size = $k$ で学習した Skip-gram モデル*3
Glove	Glove モデル*4
SVD(LC)	対数共起頻度行列の特異値分解
SVC(PMI)	自己相互情報量行列の特異値分解

SGNS( $25$ )と、SGNS( $1, 5, 15$ )、Glove、SVD(LC)、SVD(PMI) との RPD を横軸に、word similarity task と word analogy task の性能の差の絶対値の合計を縦軸にとりそれぞれプロットした結果を以下の図に示します。

f:id:taijest:20201229121909p:plain:w400 — RPD とタスクにおける性能差との関係

タスクの性能差と RPD は相関しているようにみえます。各分散表現を後段タスクの入力とした場合にこのような綺麗な関係が得られるかはわかりませんが、RPD では類似している分散表現間の距離が近く計算されていると考えられます。

RPD で計算された単語の分散表現間の関係

論文では、単語の分散表現間の関係についても分析を行っています。先ほどの表に示したアルゴリズムで学習された分散表現間の距離を計算し、2次元空間にマッピングした結果を以下に示します。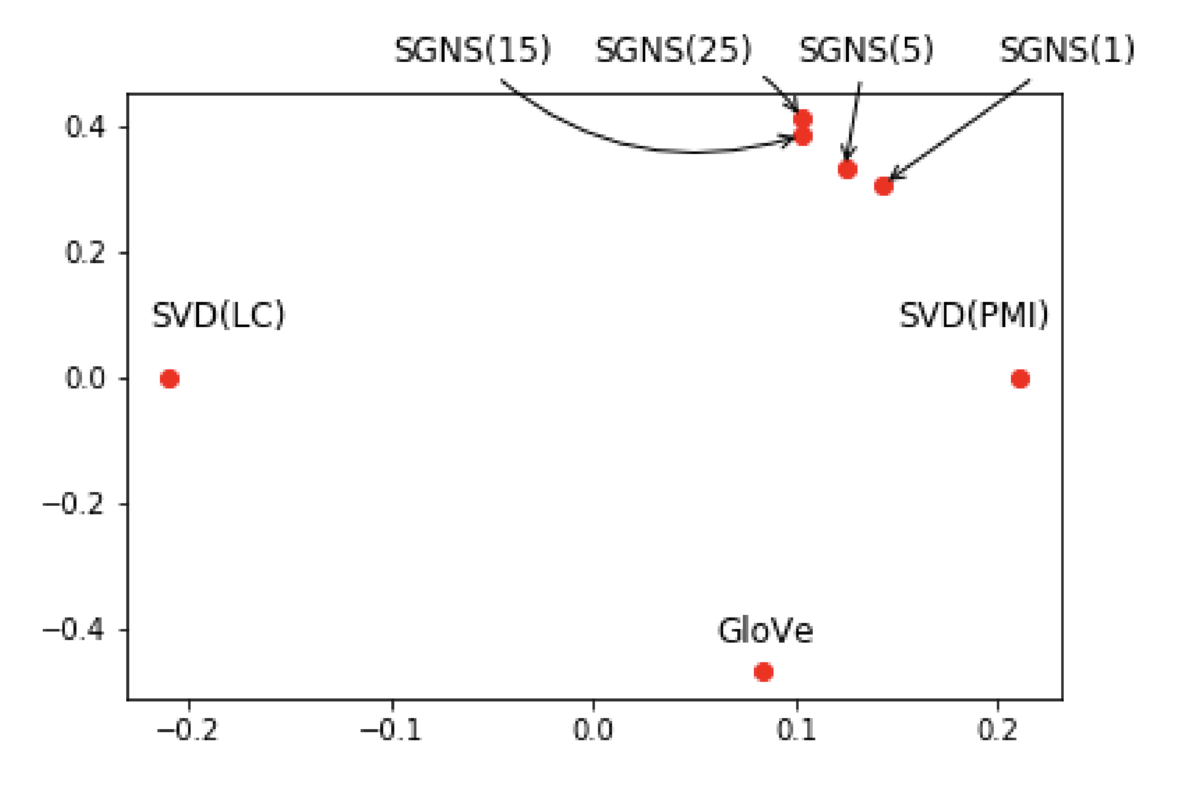

f:id:taijest:20201211231954p:plain:w400 — RPD で計算された単語の分散表現間の関係

この結果から、以下のようなことがわかります。

Skip-gram により学習された分散表現 (SGNS( $k$ )) は、他のアルゴリズムと比較して、自己相互情報量行列の特異値分解 (SVD(PMI)) と類似しています。これは、Levy et al. (2014) で示されている、「negative sampling による Skip-gram の学習は自己相互情報量行列の特異値分解と等価*5」という事実からも納得のいく結果です。
Skip-gram モデルで negative sample size を変化させたとき、得られる分散表現の性質が変わっていることが確認できます。negative sample size が大きくなるにつれ、得られる分散表現は他のアルゴリズムで学習された分散表現と類似しなくなるという傾向がみられます。

ノードの分散表現の学習アルゴリズム

さて、論文では単語の分散表現の関係を分析していましたが、本ブログでは RPD を用いて、グラフデータに対するノードの分散表現の学習アルゴリズムの関係性の分析を行います。グラフデータはそのデータ構造が複雑であるため、様々なノードの分散表現の学習アルゴリズムが提案されています。ノードの分散表現の概要や代表的なアルゴリズムについては、DSOC 研究員黒木による記事で説明されています。
本記事で分析対象とするアルゴリズムは以下の通りです。

DeepWalk
DeepWalk*6 はシンプルなノードの分散表現の学習アルゴリズムです。各ノードを始点としてグラフ上でランダムウォークを行い、得られたノードの系列を入力とした Skip-gram モデルでノードの分散表現を学習します。ランダムウォークを行うため、離れた位置のノードペアに対しても類似性を仮定しやすいのが特徴です。

node2vec
node2vec*7 は DeepWalk を改良したアルゴリズムとして提案されています。DeepWalk がグラフ上をランダムウォークするのに対して、node2vec では二種類のパラメータによりノードの遷移確率を制御することができます。これにより、周辺のノードを優先したサンプリングや、離れたノードを優先したサンプリングを実現することができます。

LINE
LINE*8 では、隣接行列をもとにノードの分散表現を学習します。ノード同士が接続しているという一次の近接性と、同じノードを共有しているという二次の近接性に基づいて損失関数を定義し、それぞれを最適化することで得られた分散表現を統合します。ランダムウォークベースの手法と比較して、周辺のノードにのみ類似性を仮定していることが特徴です。

Grarep
Grarep*9 は、異なる $k$ に対して、 $1 \sim k$ ステップ遷移確率行列から定義される類似度行列をそれぞれ特異値分解して得られた表現を結合することで、より大域的な情報を考慮した分散表現を獲得するアルゴリズムです。論文では、後段タスクの入力として評価することで、DeepWalk や LINE に対する優位性を示しています。

SDNE
SDNE*10は LINE と同様に一次の近接性と二次の近接性を考慮した損失関数を定義します。LINE との違いは Autoencoder の構造に基づいて学習を行い、隣接ノードの非線形変換により分散表現を獲得することや、一次の近接性と二次の近接性を同時に考慮して一つのネットワークで学習することです。

Graph Factorization
Graph Factorization では、隣接行列を行列因子分解してノードの分散表現を学習します。ノード数を $V$ として、 $V \times V$ の隣接行列を $V \times s$ の因子行列の積に分解し、因子行列の各行の $s$ 次元ベクトルが各ノードの分散表現になります。

NetMF
NetMF*11 では、DeepWalk や LINE などの手法と等価であるような行列の特異値分解を考えています。本ブログでは、DeepWalk と等価な行列の特異値分解を用います。具体的には、 $i$ 行 $j$ 列の要素 $x_{i,j}$ が以下で表される行列 $X$ を特異値分解します。

$\displaystyle x_{i,j} = \log\left(\frac{U}{kT}\left(\frac{1}{d_j}\sum_{r=1}^{T}(P^{r})_{i,j}\right)\right)$

$U\hspace{1mm}$ : 隣接行列の要素の和
$k\hspace{2mm}$ : DeepWalk の negative sample size
$T\hspace{1.3mm}$ : DeepWalk のランダムウォークの長さ
$d_{i}\hspace{0.9mm}$ : ノード $i$ の次数
$P\hspace{1.2mm}$ : ノードの遷移確率行列

Watch Your Step
Watch Your Step*12 は、Graph Attention Network*13 に発想を得たノードの分散表現アルゴリズムです。DeepWalk や LINE などのアルゴリズムでは、ある距離のノード間に仮定される類似度の期待値はハイパーパラメータにより学習前に決定されますが、Watch Your Step では仮定する類似度をパラメータとして学習します。つまり、学習対象のグラフに応じて、近傍のノードのみに類似性を仮定するべきか、離れているノードにも類似性を仮定するべきかをパラメータチューニングなしで考慮することができると主張しています。

ProNE
ProNE*14 は、ノードの分散表現を高速に学習するために開発されたアルゴリズムです。このアルゴリズムでは、randomized tSVD により高速に類似度行列を分解し、得られた表現をネットワーク上で伝播させることでグラフのグローバルな情報を考慮した分散表現を得ます。

[実験] RPD でノードの分散表現間の関係を計算してみる

ここからは、論文で分析されているように、ノードの分散表現間の距離を計算し、2次元空間にマッピングをしてみます。学習データには、ソーシャルブログ上のユーザー間の友人関係を表した BlogCatalog を用います。学習データのノード数は 10,312、エッジ数は 333,983 です。OpenNE、StellarGraph、Karate Club、ProNE を用いて各アルゴリズムを実装し、特に断りのない限りはデフォルトのパラメータを用いるものとします。ただし、分散表現の次元数は 128 に統一しています。各分散表現アルゴリズムでは 5 回学習を行い、RPD の計算は平均値を利用しています。

なお、本記事の実験のソースコードはこちらで公開しています。

RPD に基づくノードの分散表現間の関係を 2次元空間にマッピングした結果を以下に示します。scikit-learn の多次元尺度構成法で可視化を行っています。

f:id:taijest:20210116233310p:plain — RPD で計算されたノードの分散表現間の関係

この図からいくつかのことがわかります。

一次の近接性
LINE-1 とは、LINE において隣接しているノードの類似性 (一次の近接性) を仮定することで得られる分散表現です。LINE-1 と近しいアルゴリズムとして、ProNE が見受けられます。ProNE では、後述するような二次の近接性に基づいた類似度行列の分解を行いますが、行列分解で得られた分散表現をグラフ上で伝播させるため、結果として隣接したノードの分散表現が似ているものになっていると考えられます。

二次の近接性
LINE-2 は、LINE において隣接ノードを共有するノードの類似性 (二次の近接性) を仮定することで得られる分散表現です。LINE-2 と近しいアルゴリズムとして、LINE-1 と LINE-2 を結合した分散表現である LINE-1+2 や、Graph Factorization、SDNE、Watch Your Step などがあることがわかります。
LINE-1+2 が、LINE-1 と LINE-2 の中間ではなく、LINE-2 と近くなることは意外でした。ここで、LINE-1 は近いノードとの類似性、LINE-2 は近いノードおよび少し離れたノードとの類似性を仮定していると極端に考えると、LINE-1 と LINE-2 を結合した LINE-1+2 が LINE-2 と近くなることは少し理解できる気がします。
他のアルゴリズムについても、Graph Factorization は隣接行列を行列因子分解しているので、隣接ノードを共有するノード間の類似度が高くなること考えられますし、SDNE は一次の近接性と二次の近接性を仮定して学習を行っているため LINE-1+2 と同様の解釈ができます。
しかし、Watch Your Step では二次の近接性を仮定しておらず、ノード間の距離ごとにどの程度の類似度を仮定するかをパラメータとして学習します。今回の結果を踏まえると、グラフ全体として表現しやすいノード間の類似性を仮定した結果、二次の近接性を考慮したアルゴリズムと類似した分散表現が得られたということになります。

DeepWalk と node2vec
DeepWalk ではハイパーパラメータとして、ウィンドウサイズ $w$ を変化させて実験を行っています。また、node2vec ではハイパーパラメータ $p, q$ を変化させて、周辺のノードを優先したランダムウォーク ( $p=2, q=0.5$ )、離れたノードを優先したランダムウォーク ( $p=0.5, q=2$ ) について実験しています。可視化した結果では差異があるように見えますが、実際にはハイパーパラメータを変化させた場合の距離にはほとんど差がありません。結果として、RPD の観点からは、ランダムウォークの遷移確率を制御しても得られる分散表現への影響は小さいことがわかります。

Grarep
DeepWalk や node2vec と異なり、Grarep はハイパーパラメータを変化させることで性質の異なる分散表現を学習することができています。(図だと違いがわかりにくいですが...)
具体的には、 $1 \sim k$ ステップ遷移確率行列から定義される類似度行列をそれぞれ特異値分解して結合した分散表現を得るため、 $k$ が小さいと LINE-1 や NetMF など一次の近接性を考慮した分散表現と近い分散表現を獲得し、 $k$ が大きいと LINE-2 や Graph Factorization など二次の近接性を考慮した分散表現と近い分散表現を獲得しています。
DeepWalk や node2vec と異なり、ハイパーパラメータの変化に伴い分散表現の性質が変化した理由としては、各ステップで独立に特異値分解を行っているため、 $k$ の増加に伴いよりダイレクトにグラフの大局的な構造情報を分散表現に取り入れようとしていることが考えられます。

[実験] RPD とノード分類タスクにおける性能との関係を調査する

ノードの分散表現間の距離的な関係を確認したところで、後段タスクとの性能と組み合わせて分析を行ってみます。BlogCatalog はノードに 39 種類のラベルが複数付与されているので、マルチラベル分類を行います。各ラベルについて分散表現を入力としたロジスティック回帰で One-vs-Rest の分類を行い、各ノードで確信度の高いラベルの上位から正解のラベル数ぶんだけ付与します。

各アルゴリズムで分散表現の学習→分類器学習→評価を 5 回行い、Micro-F1 と Macro-F1 を平均した結果を以下に示します。

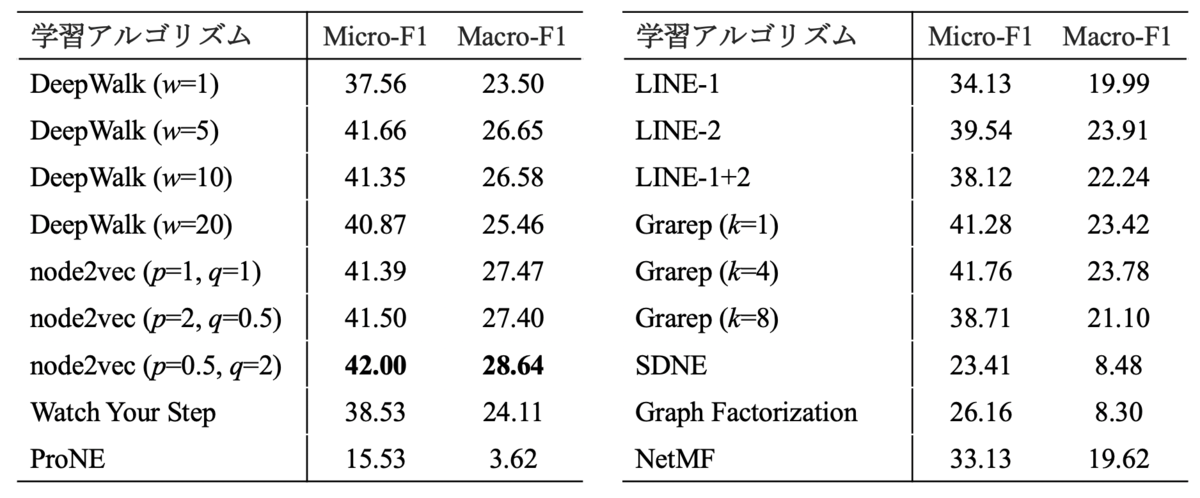
f:id:taijest:20210116232024p:plain — ノード分類タスクにおける各アルゴリズムの性能

全体的にランダムウォークを用いて学習された分散表現の分類性能が高く、この傾向は Khosla et al. (2019) で示された結果と一致します。ここで、Macro-F1 をプロットのサイズに反映させて可視化した結果を以下に示します。

f:id:taijest:20210116234919p:plain — ノードの分散表現間の関係とノード分類タスクの性能

ノード分類タスクの性能と RPD で計算された関係を重ね合わせると、LINE-2 と Graph Factorization のように、二次の近接性を仮定したアルゴリズム間でも性能の差異があることがわかります。RPD はノードペアの類似度に基づいて距離を計算していますが、ノード分類ではより大局的なノードの関係性が重要ということでしょうか。
今回は試していませんが、リンク予測はノードペアの類似度を正しく評価することが重要なタスクなので、その性能と RPD の関係が強くみられるかもしれません。

さいごに

本記事では、分散表現間の距離尺度である RPD に基づいて、ノードの分散表現アルゴリズムの関係を分析しました。最後の図でも示した通り、RPD を用いることで、後段タスクでの性能とは違った視点で分散表現を眺めることができると思います。本記事では代表的なノードの分散表現を取り扱いましたが、まだ実験できていないアルゴリズムがたくさんあります。ぜひ、お気に入りのアルゴリズムをプロットしてみてください。
では、長くなってしまいましたが、ここまで読んでいただきありがとうございました。

*1:単語ペアの類似性を推定するタスク (URL)

*2:王子 - 男 + 女 → 姫のようなアナロジーを解くタスク (URL)

*3:T. Mikolov, I. Sutskever, K. Chen, G. Corrado and J. Dean, "Distributed representations of words and phrases and their compositionality", in NIPS, 2013.

*4:J. Pennington, R. Socher and C. D. Manning, "GloVe: Global Vectors for Word Representation", in EMNLP, 2014.

*5:実際にはいくつかの仮定を置いた場合に等価となります。

*6:B. Perrozi, R. Al-Rfou and S. Skiena, "DeepWalk: Online Learning of Social Representations", in KDD, 2014.

*7:A. Grover and J. Leskovec, "node2vec: Scalable Feature Learning for Networks", in KDD, 2016.

*8:J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan and Q. Mei, "LINE: Large-scale Information Network Embedding", in WWW, 2015.

*9:S. Cao, W. Lu and Q. Xu, "GraRep: Learning Graph Representations with Global Structural Information", in CIKM, 2015.

*10:D. Wang, P. Cui and W.Zhu, "Structural Deep Network Embedding", in KDD, 2016.

*11:J. Qiu, Y. Dong, H. Ma, J. Li, K. Wang and J. Tang, "Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec", in WSDM, 2018.

*12:S. Abu-El-Haija, B. Perozzi, R. Al-Rfou and A. Alemi, "Watch Your Step: Learning Node Embeddings via Graph Attention", in NIPS, 2018.

*13:Graph Attention Network は、DSOC 研究員吉村による記事で解説されています。

*14:J. Zhang, Y. Dong, Y. Wang, J. Tang and M. Ding, "ProNE: Fast and Scalable Network Representation Learning", in IJCAI, 2019.

Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信