
こんにちは、研究開発部のDataAnalysisグループの糟谷勇児です。
今回は、統計学について書いていこうと思います。ただし今回の対象は研究員の方ではなく、統計学初心者の方を想定しています。
皆さんはスマホのゲームはやりますか?
最近はガチャでアイテムやキャラをゲットするゲームが多いですよね。
私もガチャが大好きです。
ガチャはいいですね。モンスターハンターなどのゲームも好きですが、最強の武器を手に入れるのはいつも一番強い敵を周回して素材を集めた後で、それ以上倒しに行きたい敵がいなかったりします。
しかしガチャは運次第では最初から最強のぶっ壊れキャラを引くことができるのです。
ところで、私の趣味はガチャの期待値計算をして某巨大掲示板に投稿することです。
そんな生活をしていて思いついてしまいました!
「ガチャだけで大体の統計学を学べるんじゃね?」
統計学はギャンブルから生まれたともいわれていますのでガチャとは相性がいいはず。
というわけで、一緒にガチャで統計学を学んでデータに強くなりましょう(研究者や統計学に強い方の突っ込みはご遠慮ください)。
単発ガチャ(1連ガチャ)と10連ガチャの確率
皆さんのやっているゲームのガチャでSSや星5などの最高レア度のアイテムやキャラが出る確率は何パーセントでしょうか。
私がやっているドラクエウォークでは星5は7%の確率で出ます(さらに、そこからピックアップという今回目玉のアイテムが出る確率は 20%ぐらいなので、1.4%ということになり、加えてそれが武器の確率は...)。
ここでは7%として話を進めていきます。
つまり単発のガチャを引くと93%で星4以下のはずれ、7%で星5のあたりということです。
これをグラフに書いてみるとこんな感じです。

ちょっと数学っぽく関数で書いてみます。はずれは0、あたりは1とすると
f(0) = 0.93
f(1) = 0.07
となります。
このように関数にして、起きること(当たり:1, 外れ:0)とその確率を対応付けたものを確率関数と呼びます。
(このブログではもうこの言葉は出てこないかもしれません)
また、0と1のような2パターンではなく、「人間の身長」というような連続した値(連続値)を入れる関数も作れます。連続値を入力とするものは確率密度関数と呼びますが、このブログはガチャがすべてなので連続値のことは考えません。
確率関数と確率密度関数をひっくるめて確率分布と呼びます。
そして、f(0)とf(1)の2パターンの一定の確率を返す確率分布をベルヌーイ分布と呼びますが、ベルヌーイ分布と呼んでもなんだったっけってなると思うので、ここでは1連ガチャ分布(ベルヌーイ分布)と書くことにしましょう。※ググりやすいように併記してみました
100円玉を投げて裏が出る確率をf(0)、表が出る確率をf(1)としても1連ガチャ分布(ベルヌーイ分布)です。
この場合はだいたい
f(0) = 0.5
f(1) = 0.5
となります。
さて、ガチャを1連でやる人はあまりいないかもしれません。10連のほうがお得なことが多いですからね。
そこで、10連したときに星5が出る個数とその確率を考えてみましょう。星5確定などはないとします。
皆さんの中で、10個全部星5が出たことがある人いますか?いないですよね。つまり0%です...ではなく微粒子レベルでその可能性は存在します。
つまり、毎回7%のほうに入ればいいので7%×7%×...×7%=7%の10乗=0.00000000028%、1000億回ぐらい10連ガチャをすれば3回ぐらいあるかもしれません。
つまり、f(10) = 0.00000000028%
9個出る確率は7%の9乗×93%×10(何回目で当たるか)で...毎回計算するのは大変なのでExcelでやってみます。
0.0000000375%のようです。
何気なくExcelを使ってみましたが、私も昔は使えなくて友達に「まずセルの中に=って打てばいい」
と教わって使えるようになりました。
セルの中に=と打つと計算式を扱うモードになるのでそのあとで計算式を打ち込むのです。
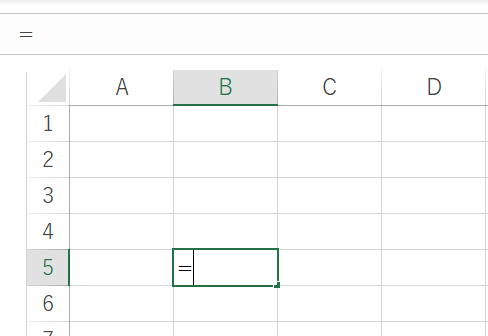

(^は累乗の記号、 *は掛け算の記号)
さて、このように、同じ確率で当たりが出るくじを何回か引いた時に当たりの数に対する確率を、二項分布と言います。
二項分布と言われても何のことだっけってなると思うのでN連ガチャ分布(二項分布)と書くことにしましょう。
グラフを書くとこんな感じです。

N連ガチャ分布(二項分布)を計算してくれるサイトもあるのでガンガン利用しましょう。
Excelでは=BINOM.DIST(3, 10, 0.07, FALSE)
等と書きます。10が10連を表し、3が当たり数を表します。0.07が当たり率でFALSEは通常の確率分布の値を使うというパラメーターです。

実際の例
ちなみに私は10連で5枚の星5をゲットしたこともあります。
これがどれだけ珍しいかというと、f(5)=0.029%ですので、10000回10連ガチャを引けば3回ぐらいということになります。
ユーザーが10万人ぐらいいるサービスだったら、毎回30人ぐらいは5枚抜きしていることになるわけです。
某大型掲示板を見ていると「あいつは運営のお友達だ」みたいなことが言われたりもしますが、実際大当たりする人もいるのが普通の認知と異なるところかもしれません。
どんなにレアなキャラでもフレンドに一人ぐらいは一発で当てる人がいるのはこのためです。
実は無課金を装ってるけど課金兵じゃねみたいなことを言ってはいけません。
終わりに
そんなわけで、初回は1連ガチャ分布(ベルヌーイ分布)とN連ガチャ分布(二項分布)の紹介でした。
でも確率分布っていっぱいあるって大学で習ったような...。2つだけじゃ役に立たないんじゃない?
と思う方もいると思いますがそんなことはありません。
この二つを使いこなすだけで、ゲームのガチャも普段の業務も部活も進研ゼミもすべてうまくいくのです(個人の感想です。また、データサイエンティストのような業務には当てはまらないかもしれません)。
そんなわけでこれからガチャをしながら確率を一緒に勉強していきましょう。