Hi, I am XING LI, a researcher from Sansan DSOC.
Last time, we briefly discussed the DGL(Deep Graph Library) and one of its fundamental mechanisms: Message Passing. Today, we are going to explore another significant data structure: NodeFlow.
NodeFlow
For more convenient discussion, we will create a demo graph and talk based on it. A classical demo graph is the famous "Zachary’s karate club"
A social network of a karate club was studied by Wayne W. Zachary for a period of three years from 1970 to 1972[1]. The network captures 34 members of a karate club, documenting links between pairs of members who interacted outside the club. During the study a conflict arose between the administrator "John A" and instructor "Mr. Hi" (pseudonyms), which led to the split of the club into two. Half of the members formed a new club around Mr. Hi; members from the other part found a new instructor or gave up karate. Based on collected data Zachary correctly assigned all but one member of the club to the groups they actually joined after the split.
First, we create a demo graph and illustrate it:
import dgl import networkx as nx import numpy as np import matplotlib.pyplot as plt %config InlineBackend.figure_format = 'svg' def build__graph(): src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21, 25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33]) dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4, 5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23, 24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]) # Edges are directional in DGL by default; We forcely make them bi-directional here. u = np.concatenate([src, dst]) v = np.concatenate([dst, src]) # Construct a DGLGraph return dgl.DGLGraph((u, v)) G = build__graph() print(G) # ===== OUTPUT ===== # DGLGraph(num_nodes=34, num_edges=156, # ndata_schemes={} # edata_schemes={}) # The actual graph is undirected, we convert our bi-directional graph to undirected here. nx_G = G.to_networkx().to_undirected() pos = nx.kamada_kawai_layout(nx_G) nx.draw(nx_G, pos, with_labels=True, node_color=[[.5, .5, .5]])
This is a relatively tiny graph that only contains 34 nodes and hundreds of edges. Therefore, to learn the embedding for a certain node in this graph by GCN(Graph Convolutional Networks), we could convolute all nodes at one time. However, as the graph scales up to billions of nodes or edges, training on the whole graph would no longer be efficient or even feasible. The questions out of the same nature are faced in any other large scale machine learning area, one typical solution is mini-batch. Inspired by this, in DGL, mini-batch training allows you to control the computation and memory usage within some budget.
In the karate club example, if we want to apply convolution operation on node 16. We could image a two-layer subgraph grows from the
seed node 16:
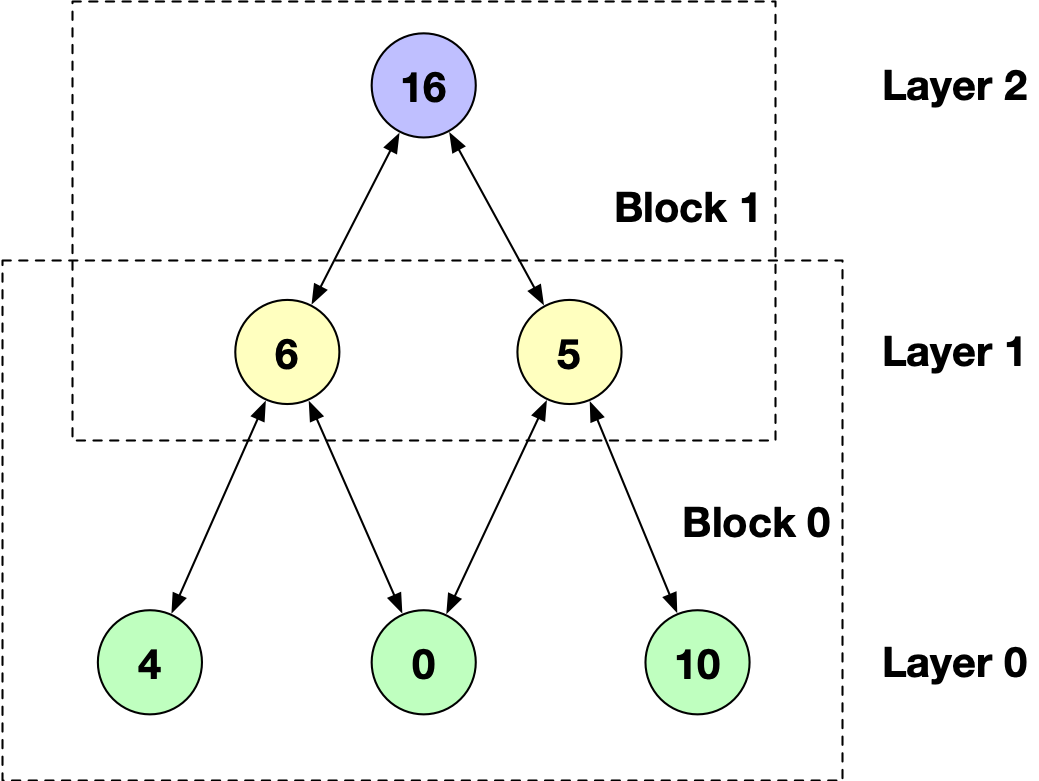(Here, each node could only be sampled once.)
This is the so-called NodeFlow data structure. To build it from a DGLGraph, DGL provides two functions:
dgl.contrib.sampling.sampler.NeighborSampler(g, batch_size, expand_factor=None, num_hops=1, neighbor_type='in', transition_prob=None, seed_nodes=None, shuffle=False, num_workers=1, prefetch=False, add_self_loop=False)
and
dgl.contrib.sampling.sampler.LayerSampler(g, batch_size, layer_sizes, neighbor_type='in', node_prob=None, seed_nodes=None, shuffle=False, num_workers=1, prefetch=False)
The main difference between them is the LayerSampler has explicit restrictions on each layer's size. This may be more efficient in two technical aspects. "First, we can reuse the information of the sampled neighbourhoods since the nodes in the lower layer are visible and shared by their different parents in the upper layer. Second, it is easy to fix the size of each layer to avoid over-expansion of the neighbourhoods, as the nodes of the lower layer are sampled as a whole."[2] More information about these two methods could be found in this paper.
Let's try NeighborSampler while the seed node contains only 16:
from dgl.contrib.sampling.sampler import NeighborSampler #DGL now only supports the immutable graph, make sure the graph is in read-only state. G.readonly(True) nodeflow_loader = NeighborSampler(g=G, batch_size=2, expand_factor=10000, num_hops=2, seed_nodes=[16]) for subgraph in nodeflow_loader: print(subgraph.layer_parent_nid(2)) print(subgraph.layer_parent_nid(1)) print(subgraph.layer_parent_nid(0)) # Here, we did not remove the repeat nodes # ===== OUTPUT ===== # tensor([16]) # tensor([5, 6]) # tensor([ 0, 4, 5, 6, 10, 16])
One special thing to mention here is if the graph contains node featuresor edge features, please remember to copy these features values from the parent graph and vice verse. You only need add one more statement after creating the NodeFlow just like:
from dgl.contrib.sampling.sampler import NeighborSampler G.readonly(True) nodeflow_loader = NeighborSampler(g=G, batch_size=2, expand_factor=10000, num_hops=2, seed_nodes=[16]) for subgraph in nodeflow_loader: subgraph.copy_from_parent() # ...Codes use node/edge features... # If you want to update the corresponding features from NodeFlow to parent graph subgraph.copy_to_parent()
After creating NodeFlow loader and copy_from_parent(). You can query the structure and features information of each NodeFlow or apply computing operations on it, including the Message Passing functions.
Most query functions are straightforward, while the computing operations are relatively complicated. The computing operations involve the callable function parameters Edge UDF and Node UDF. Details on these UDF(user-defined functions) could be found in previous blog at Message Passing section.
Now, you have grasped all necessary knowledge over DGL to build a graph convolutional networks with mini-batch method. A fundamental task in graph learning is sampling which includes positive and negative sampling methods, just like the NodeFlow also heavily relies on the default sampling method. Because sampling is so common and computing-intensive, people always implement it by C++/C to speed it up. In the next blog, we will explore and compare different sampling methods, especially various negative sampling methods and discussed some related topics.
References
[1] Zachary, W. W. (1977). "An Information Flow Model for Conflict and Fission in Small Groups". Journal of Anthropological Research. 33 (4): 452–473. JSTOR 3629752.
[2] Huang, Wenbing, et al. "Adaptive sampling towards fast graph representation learning." Advances in neural information processing systems. 2018.
