f:id:sansan_yoshimura:20210222095528p:plain DSOC 研究員の吉村です. 最近非常においしいと評判の,とあるジャムを手に入れました. ジャムだけあっても仕方ないので, せっかくなのでトースターも合わせて買ってみました. 焼いたパンに美味しいと評判のジャムが合うのかどうか, 食べるのが待ち遠しいです.

さて, 今回は Factorization Machines (FMs) [*1] についての話です. FMs は広告配信の文脈において CTR (Click Through Rate ) の予測などに用いられる手法です. 利点は, Sparse なデータに対しても高速に処理を行うことができる点です. 一方で, ナイーブな FMs ではメモリ効率が悪いという課題があるため, Rendle 氏が 2010 年に提案してから, 現在までに様々な派生が生まれています. 今回は, そうした派生に目を向けながら話を進めていきます.

下記は本記事の目次です.

Factorization Machines (FMs) とは
FMs の応用
FMs の派生
まとめ

Factorization Machines (FMs) とは

冒頭で説明したように FMs は Rendle 氏によって 2010 年に提案されています. FMs は各特徴量間の二次の相互関係までを含めたモデルで, 下記の式で表すことができます.

$\displaystyle \hat{y}_{\text{FMs}} (\boldsymbol{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n\sum_{j=i+1}^n \langle \textbf{v}_i, \textbf{v}_j \rangle x_ix_j \tag{1}$

ただし, $\displaystyle \boldsymbol{x}\in\mathbb{R}^n$ は入力となる $n$ 次元特徴量を表し, $w_0$ , $w_i$ , $\textbf{v}_i \in \mathbb{R}^k$ $(i=1, \cdots, n)$ は学習パラメータを表します. 式 (1) の第三項の部分が, 上述した二次 (second-order) の相互関係を考慮している部分に該当します. この第三項を愚直に計算すると $\displaystyle O ( kn^{2} )$ の計算量が必要になりますが, 再定式化をして次の等価な表現に書き換えることによって, 計算量を $\displaystyle O(kn)$ まで抑えることができます.

$\displaystyle \sum_{i=1}^n\sum_{j=i+1}^n \langle \textbf{v}_i, \textbf{v}_j \rangle x_ix_j = \frac{1}{2} \sum_{f=1}^k \left[ \left( \sum_{j=1}^n v_{j, f} x_j \right)^2 - \sum_{j=1}^n v_{j, f}^2x_j^2 \right] \tag{2}$

学習には SGD (Stochastic Gradient Decent) を用いています. 式 (1) を見てわかるように, FMs では直接相互関係の重みを学習するのではなく, 各特徴量の latent vector (内部で持っている埋め込みベクトル) を学習することにより, テスト時に初出の組み合わせであってもそれなりに意味のある予測ができることが利点となります. そのため, one-hot による前処理を行うことが多いという理由で Sparse になりやすい Categorical データを多く含むようなデータセットにおいても, うまく学習し予測できるところが FMs の強みと言えます.

また, 二次の相互関係までを見ているのであれば, 三次以降の相互関係も見てみたいというのは自然な発想です. [Rendle, 2010] では, この二次までを考慮する FMs を 2-way FMs と呼び, これを一般化した d-way FMs の定式化も提案しています.

FMs の応用

Sparse なデータに対して有用であるという話を上述しましたが, 実際にはどのような応用があるのでしょうか? 先にも述べたように, 一番よく見られる応用先は CTR 予測です. CTR 予測の問題設定を簡潔に説明すると, ユーザと広告それぞれの特徴量を一つの行に並べて, そこから CTR を予測するというタスクと言えます.

他の応用先として, 例えば推薦の文脈では, cross-domain の商品推薦のアルゴリズム [*2] などが挙げられます. ここで言っている cross-domain というのは, 例えば, EC ショップのデータと, SNS のデータとの間を橋渡しして, 商品推薦をするという意味合いが込められています. しかし, これら二つの間に共通して存在するユーザは必ずしも多くないため, データが Sparse になることが想像され, その点において FMs の適用が威力を発揮することになります.

その他には NLP の文脈では, Open Relation Extraction (Open RE) と呼ばれるタスクにおいての利用が見られます [*3]. Open RE は, 二つの Entity ( $E$ ) の組 ( $T \subseteq E \times E$ )とその間の Relation ( $R$ ) を考えたときに, 順序付けられた (ranked) Entity 集合 $T_r \subseteq T, r \in R$ を返すことが目的となります. この時, $T_r$ は Relation $r$ の関係についての Entity のペアを表し, 訓練時に観測されていない Relation $r$ を持つ Entityの組 $t \in T$ を要素に持つという制限があります. この時, 正しい事実 ( $t$ と $r$ の組合せ) の方が誤った事実よりも順位が高い出力が良い出力ということになります. Entity や Relation については下記でも取り扱っていますので, 合わせてご覧ください.

buildersbox.corp-sansan.com

FMs の派生

ここでは, FMs の派生についてまとめていきます. 今までに非常にたくさんの FMs の派生手法が生まれていますが, その中でもある程度ターニングポイントだと思ったもののみをその関係も合わせて図にしたものが下記になります. なお, 括弧で書いているものは FMs ではないものの影響を与えたものを記載しています.

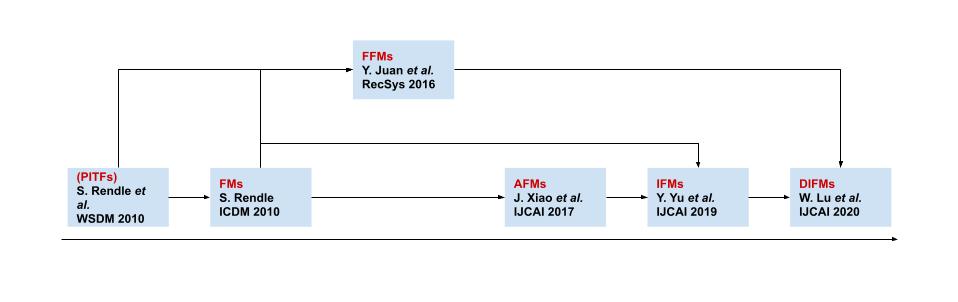
f:id:sansan_yoshimura:20210409135445j:plain — FMs の提案の時系列的順序と, 関連の概略図.

Field-aware Factorization Machines (FFMs)

Field-aware Factorization Machines (FFMs) [*4] は, FMs に Fields と言う概念を取り入れたモデルで, FMs の拡張でありPITFs [*5] の一般化手法と位置付けることができます. 基本の FMs では latent vector を各特徴量ごとに暗黙的にモデリングしていましたが, [Y. Juan, 2016] では特徴量を Fields と呼ばれるものにグループ分けして, Fields ごとに別の latent vector を持たせるようにすることで性能向上が図られています. 具体例で言えば, ウェブサイトにユーザが自分の情報整理のためにタグをつける状況において, 適切なタグを推薦するタスクを考えます. (ちなみに, この場合に "user" と "website" と "tag" からなる 3 階のテンソルを特殊な方法で分解し, そこで得られた latent vector の内積によってこの三つの相互関係を表現するのが PITFs です.) この時, 特徴量として考えられるのは, ユーザの特徴量, ウェブサイトの特徴量, そして, タグを表す特徴量の三つです. 基本の FMs ではこれらを concat して扱うわけですが, FFMs では "user", "website", "tag" というような Fields に先にグループ分けをしておいて, これらの間の二項間の関係それぞれに対して, 各特徴量に別の latent vector を持たせます. つまり, この場合は "user" のある一つの特徴量に対応する latent vector は, 対 "website" と対 "tag" で別の表現になるということを言っています. したがって, "user" Field に属する特徴量 $x$ は次の二つの latent vectors $\textbf{v}^{website} , \textbf{v}^{tag}$ の二つの latent vector を持つことになります. 予測時における理論的な時間計算量は大きくなりますが, ハイパーパラメータである latent vector の次元は基本の FMs に比べるとずっと小さい値で良いため, 実験的にはそれほど計算量が大きくなるわけではないようです. FFMs については, Numerical Features の扱いが少し特殊になるため, その辺りは工夫が必要になります.

Attentional Factorization Machines (AFMs)

Attentional Factorization Machines (AFMs) [*6] は, FMs に Attention 構造を導入することにより, 各相互関係ごとに重みを変更することで性能向上を図った手法です. Attention 機構を導入していることから, モデルがより解釈しやすくなっていると主張されています.

Input-aware FMs (IFMs)

Input-aware FMs [*7] は, AFMs の一般化にあたる手法です. AFMs では各相互関係ごとに重みを変えるというところが意識されていましたが, IFMs では入力となる instance ごとに内部の重みを変えるというところに意識があります. したがって, IFMs では一次 (first-order) の項の重みと各 latent vector のサイズを, Attention-like な Factor Estimating Network (FEN) という構造を用いて reweight します.

Dual Input-aware FMs (DIFMs)

Dual Input-aware FMs (DIFMs) [*8] は IFMs の表現力をさらに上げるために様々なコンポーネントを追加したモデルです. IFMs で FEN で達成していた各入力に合わせて適応的に重み付けをしていく部分は, multi-head attention を用いています. この, 適応的に重み付けする部分には field-aware である vector-wise なものと, そうでない bit-wise なものの二通りを同時に考慮しており, これらの組み合わせにより現段階で state-of-the-art を達成しています.

その他

今回は量が多くなりすぎるという理由から紹介しきれなかったものとして, high-order な場合を (暗黙的に) 考慮する DeepFMs [*9]や, 明示的に考慮する eXtreme Deep FMs (xDeepFMx) [*10] や, latent vector のランクを固定から柔軟なものにした Rank-aware FMs (RaFMs) [*11] なども提案されています. この他にも大量の FMs 関連手法は提案されていますので, ご興味があれば探してみると面白いと思います.

まとめ

今回は Factorization Machines (FMs) についての外観をまとめました. 応用としては CTR 予測だけではなく, cross-domain な文脈での推薦や, OpenRE と呼ばれる NLP のタスクなどでも利用されていることを確認しました. また, FMs の派生として, 個人的に重要だと判断したものについていくつかピックアップして, その流れとともにそれぞれの手法の update 部分を説明しました.

今回も読んでいただきありがとうございました. 次回はまた別の内容でお届けする予定です. 是非, 読者になるボタンを押して, 読者になってみてください！

▼【ML Tech RPT. 】シリーズ buildersbox.corp-sansan.com

*1:S. Rendle, "Factorization Machines," ICDM, in 2010.

*2:X. Wang, X. He, L. Nie and T. S. Chua, "Item Silk Road: Recommending Items from Information Domains to Social Users," SIGIR, in 2017.

*3:F. Petroni, L. D. Corro, and R. Gemulla. "Core: Context-aware open relation extraction with factorization machines," EMNLP, in 2015.

*4:Y. Juan, Y. Zhuang, W. S. Chin, and C. J. Lin, "Field-aware factorization machines for ctr prediction," RecSys, in 2016.

*5:S. Rendle and L. Schmidt-Thieme, "Pairwise interaction tensor factorization for personalized tag recommendation," WSDM, in 2010

*6:J. Xiao, H. Ye, X. He, H. Zhang, F. Wu, and T. S. Chua, "Attentional factorization machines: Learning the weight of feature interactions via attention networks," IJCAI, in 2017.

*7:Y. Yu, Z. Wang, and B. Yuan, "An input-aware factorization machine for sparse prediction," IJCAI, in 2019.

*8:W. Lu, Y. Yu, Y. Chang, Z. Wang, and C. Li, "A Dual Input-aware Factorization Machine for CTR Prediction", IJCAI, in 2020.

*9:H. Guo, R. Tang, Y. Ye, Z. Li, and X. He, "Deepfm: a factorization-machine based neural network for ctr prediction," IJCAI, in 2017.

*10:J. Lian, X. Zhou, F. Zhang, Z. Chen, X. Xie, and G. Sun, "xdeepfm: Combining explicit and implicit feature interactions for recommender systems," KDD, in 2018.

*11:X. Chen, Y. Zheng, J. Wang, W. Ma, and J. Huang, "RaFM: Rank-Aware Factorization Machines," ICML, in 2019.

Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信

【ML Tech RPT.】第23回 Factorization Machines を学ぶ.