
DSOC 研究員の吉村です。最近はシーバスフィッシングにハマっています。長らく釣れない日々を送っていたのですが、つい最近久しぶりに釣り上げてから、調子がややよくなってきました。
さて、前置きはこのくらいにして、今回も不均衡データ学習の話です。今回は、不均衡データに対して異常検知手法を用いる方法について説明をします。ちなみに前回、前々回の記事をまだ読まれていない方はそちらから見ていただけると嬉しいです。
buildersbox.corp-sansan.com
buildersbox.corp-sansan.com
不均衡データ学習に異常検知手法を用いる場合の仮定
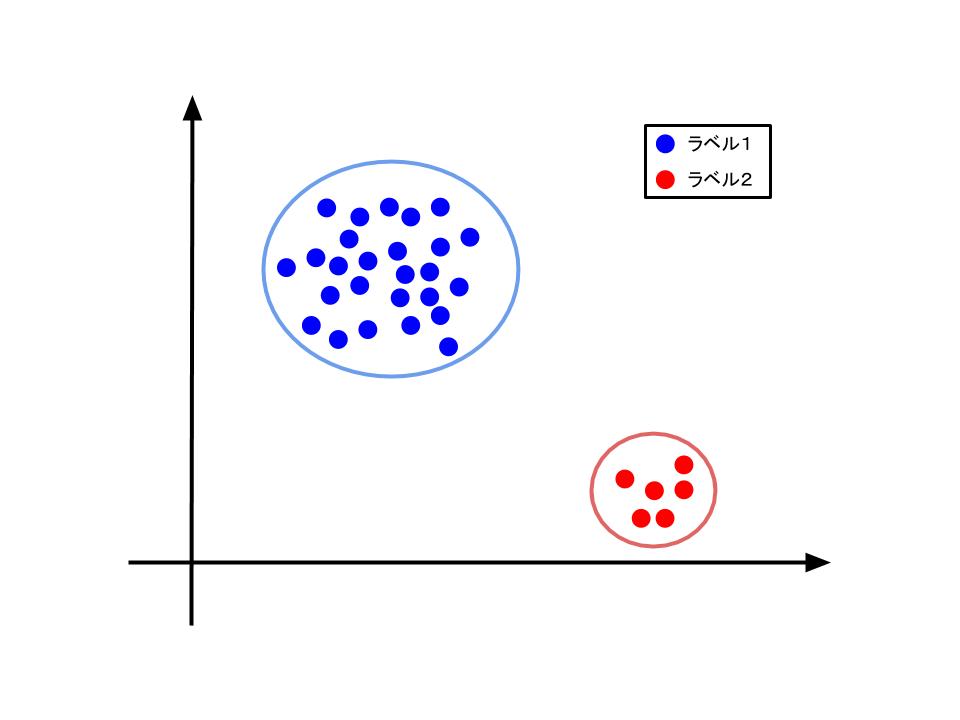
(左図) 分類問題として対処すべきと考えられるデータの分布。
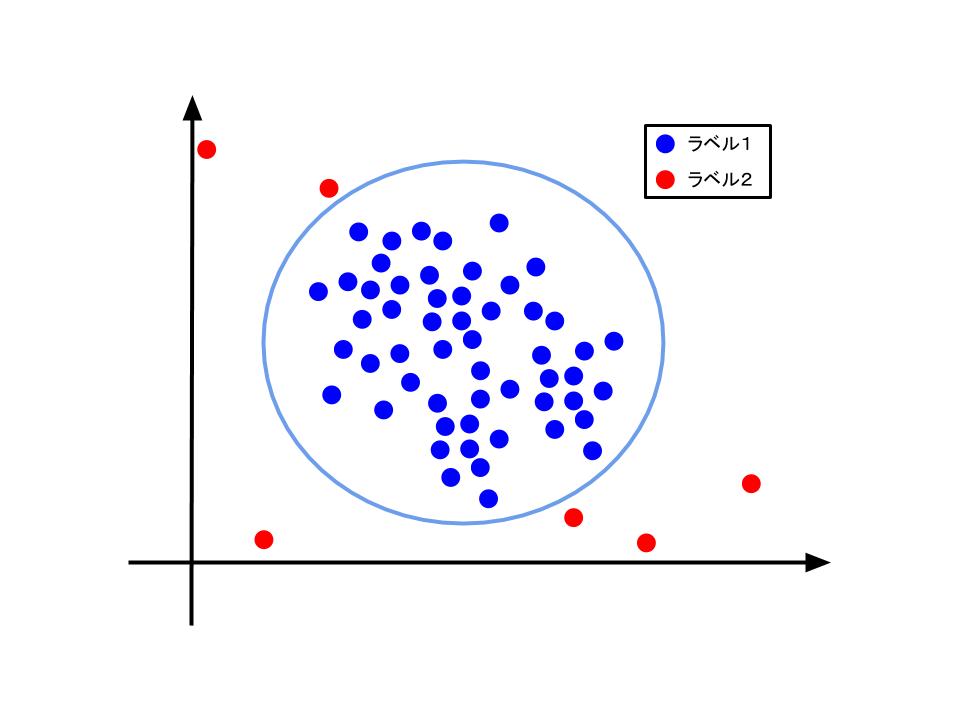
(右図) 異常検知問題として対処すべきと考えれるデータの分布。
不均衡データ対策として異常検知手法が有効に働くのは、少数派のデータ点が特徴量空間上でクラスタを作っていない場合であると考えられます。この時には、少数派のデータを"滅多にない"、"普通ではない"データ(つまり、異常データ)と考えることで異常検知手法の適用ができます。
ここで私が言いたいことは、あくまでも不均衡データ学習を異常検知の問題設定とみなせるときにのみ、異常検知手法が威力を発揮するのであり、異常検知手法は不均衡データ学習全般に対する汎用的な対処法ではないということに注意すべきであるということです。本記事の趣旨は不均衡データ学習に用いるための手法を知ることなので、今回は時系列ではない異常検知問題に対処するための手法についていくつか紹介します。
異常検知手法の三分類
異常検知手法を分類するための基準はいくつかありますが、一般的には教師あり学習、半教師あり学習、教師なし学習の三つの大きな枠組みで分類することが多いようです。念のため確認しておくと、教師あり学習は学習時に与えられる全ての事例に教師ラベルが与えられる枠組み、半教師あり学習は一部の事例に対してのみ教師ラベルが与えられ、教師ラベルが与えられない事例も多数ある場合の枠組み、教師なし学習は全ての事例に対して教師ラベルが与えられない枠組みです。これらは、直面する課題がどのようなものかによって、どの枠組みの手法を用いるかが変わります。
異常検知手法
ここでは、不均衡データ学習に利用できそうな異常検知手法を新旧を問わずいくつか紹介しようと思います。
One-class SVM
One-class SVM[*1] は教師なし学習に分類される手法です。SVM (Support Vector Machine) を1クラスの場合に改良したもので、入力として与えた (そのほとんどが) 異常ではない事例集合のうち、予め決めた割合の事例をできるだけ小さい領域で囲うことができる境界線を学習するモデルです。これにより、学習で得られた境界線外のデータを、入力として与えたデータの分布から外れている可能性が高いデータとみなすことで異常なデータ点を検出することができます。こちらはscikit-learnにも実装されています。
Local Outlier Factor (LOF)
Local Outlier Factor[*2]は、Local Outlierという外れ値を定義して、異常の有無を判別したいデータがLocal Outlierである度合いを計算することで、対象データが異常であるかどうかを判別する指標です。LOFは近傍法をベースにしており、また、計算の中ではと呼ばれる特定のデータ点からの近傍点の数を表すパラメータを一つだけ設定して用います。こちらもscikit-learnにも実装されています。
Isolation Forest (iForest)
Isolation Forest[*3]は、データ点がある空間を分割することを考えます。分割する際には、特徴量のうち一つをランダムに選び、その特徴量がとる最大値、最小値の間のランダムな値で空間を分割することを、一つの空間に一つのデータが含まれる状態となるまで繰り返します。
こうして得られる二分木を見た時に、より分割回数が多い(木の深いところに対象となるデータ点が含まれる空間のリーフがある)ものは他の"普通の"データ点と密集していると考えられるため異常ではなく、逆に分割回数が少ない(木の浅いところに対象となるデータ点が含まれる空間のリーフがある)ものは"普通の"データ点と密集していないと考えられるため、異常であると判断することができそうだという観点から異常検知をします。実際には木が一つであればバラツキが大きくなるので、データ点をサブサンプリングしたのちに、各サンプリングデータ点の集合ごとに木を作ってそれをまとめたForestを作成することで、頑健性を保っています。こちらもscikit-learnにも実装されています。
AnoGAN
AnoGAN[*4]は、Generative Adversarial Networks(GAN)を異常検知に応用した手法です。ここでは、GAN自体の詳細には踏み込みませんが、AnoGANでは(ほとんどが)"普通の"画像を元に学習することで、それまでに入力として与えられた画像の分布をGeneratorに学ばせます。その後、その"普通の"分布を学んだGeneratorを用いて生成される画像と、新たに入力として与える異常の有無を判別したい画像とを比較するような評価関数を用いることで異常度を計算します。実際には、residual score と discrimination score
とを
で調整したスコアを用います。
Deep Support Vector Data Description (Deep SVDD)
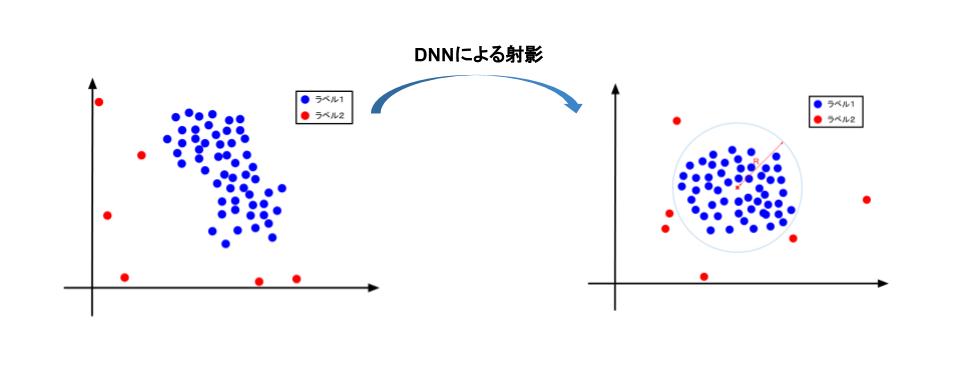
この手法では、入力は(その大部分が)"普通の"データ点であるため、教師なし学習に分類されます。[L. Ruff et. al. 2018]では、Deep SVDDのバリエーションとして明示的に超球とそれ以外の空間の境界を与えるsoft-boundary Deep SVDDと、超球の中心として定めた点からDNNによる射影後の点までの距離を異常度スコアとするOne-Class Deep SVDDが提案されています。前者は$$\min_{R, \mathcal{W}}\ \ \ \ R^2+\frac{1}{\nu n}\sum_{i=1}^n\max\{0, ||\phi(x_i;\mathcal{W})-c||^2 -R^2\} + \frac{\lambda}{2}\sum_{l=1}^L||W^l||_F^2$$という最適化問題として定式化されています。ただし、と
はそれぞれ超球の中心と半径を、
は
番目の事例を、
はDNNの各層が持つ重みパラメータ行列の集合を、
はDNNによる射影関数を、
はフロベニウスノルムを、
はハイパーパラメータを、
は重み減衰正則化パラメータを表します。後者は$$\min_R\ \ \ \ \frac{1}{n}\sum_{i=1}^n||\phi(x_i;\mathcal{W})-c||^2 + \frac{\lambda}{2}\sum_{l=1}^L||W^l||_F^2$$という最適化問題として定式化されています。ただし、変数はsoft-boundary Deep SVDDのものと同様です。学習自体は途中までは
を固定したままで先にDNNを学習するなどのテクニックはあるものの、基本的にはSGDで行うようです。[L. Ruff et. al. 2018]の中では、Deep Learningタスクのチュートリアルとしてよく知られたMNISTとCIFAR-10で実験が行われており、多くの場面でOne-Class Deep SVDDがOne-Class SVMやAnoGANを差し置いてstate-of-the-artを達成しています。
まとめ
今回は不均衡データ学習で用いることができそうな異常検知手法について、いくつか紹介しました。先にも述べたように、異常検知手法は不均衡データ学習の文脈における汎用的な手法ではないものの、状況によっては威力を発揮するのではないかと思います。こうやって手法を見ていくと、多くのものが図形的な観点からの直感的な分類方法となっており、実際に用いる場合にもデータを一度確認してからであれば威力を発揮しそうだと感じました。
さて、当連載の第4回から今回の第6回までで不均衡データ学習について見てきました。実際の業務を行う上でも、不均衡データと出会うことは多いため、そういった場面で読者の皆様のお役に立てていれば幸いです。不均衡データ学習に関しての記述は一旦今回までで終わります。
次回はまた別のトピックについてのブログを書く予定なので、気になる方は読者登録してもらえると嬉しいです。では、次回をお楽しみに。
*1:B. Schökopf, J. C. Platt, J. Shawe-Taylor, A. J. Smola, and, R. C. Williamson, "Estimating the Support of a High-Dimensional Distribution," in NC, 2001.
*2:M. M. Breunig, H. P. Kriegel, R. T. Ng, and, Jörg Sander, "LOF: Identifying Density-Based Local Outliers," in SIGMOD, 2000.
*3:F. T. Liu, K. M. Ting, and, Z. H. Zhou, "Isolation Forest," in ICDM, 2008.
*4:T. Schlegl, P. Seeböck, S. M. Waldstein, U. Schmidt-Erfurth, and, G. Langs, "Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery," in IPMI, 2017.
*5:L. Ruff, R. Vandermeulen, N. Goernitz, L. Deecke, S. A. Siddiqui, A. Binder, E. Müller, and, M. Kloft, "Deep One-Class Classification," in ICML, 2018.