f:id:komatsuna4747:20210127160740j:plain Sansan DSOC R&D 研究員の小松です。本稿では、戦略的ネットワーク形成について理解するために重要な概念を抑えたいと思います。

前回の最後に"Econometrics of Interactions in Networks"に関連したトピックについて書くと言っていました。が、現在進めている共同研究が network formation に関連したものであり、直近はそれに関連したトピックについてブログを書いたほうが学習効果が高いため、予定を変更して network formation に関連した記事をしばらく書くことにします。

前回の参考文献で言及し忘れていましたが、早稲田大学の星野先生のlecture noteは、特に econometrics of interactions in networksや spatial econometrics について大変勉強になり、おすすめです。 https://drive.google.com/file/d/1qEIXHlMYQ2KkaW5shIL8P7lMSsx2I9m_/view

Econometrics of strategic network formation のサーベイとして、De Paula (2020)、Graham (2020) などがあります。

なぜ network formation を研究するのか？

興味深いから、と言ってしまえば無責任でしょうか。それっぽい理由を探してみましょう。

モチベーションの1つとしては、人と人のつながりを表す社会的ネットワークは、個々人の socioeconomic performance の重要な決定要因だから、ということがあるでしょう。実際、教育 (Calvó-Armengol, Patacchini, and Zenou 2009)、新技術への適応 (Conley and Udry, 2010; Banerjee et al., 2013)、青少年間の risky behavior の伝播 (Nakajima, 2007)、雇用 (Topa, 2001) など、幅広い分野で social network の果たす役割に関する研究が蓄積されおり、その重要性を否定する人はまずいないでしょう。

social network は大事とは言いつつも、こうした研究は基本的にネットワークを所与のものとして扱うケースがほとんどです。しかし実際には、ネットワークは内生的に生成されるもの、言い換えると人々の何らかの意思によって形成されるものと考えるのが普通です。したがって、その背後にあるメカニズムを究明するために、ネットワークの形成をモデル化する必要性が出てくるわけです。加えてそうしたモデルの推定することで、例えば同じ属性を持った者同士はつながりやすいといった homophily が存在するかを検証することが可能となります。

ネットワーク形成のモデル化、およびその推定は困難を伴いますが、裏を返せばそこが面白く、研究の価値がありそうです。英語には便利な表現があって、こういうことを "challenging" と言えば、なんでもそれっぽく聞こえます。

ナッシュ均衡を使って戦略的ネットワーク形成を考えてみる

ひとまず、ネットワークの形成過程を研究する意義ありそうだというのはわかりました。では、その形成過程をどのようにモデル化するのでしょうか。以下の説明は Jackson (2008) の Chapter 6 に依ります。

古典的なモデルとしては、Erdős-Rényi random graph があります。これは、ネットワークの各リンクが形成される確率が、各エッジごとに独立である確率 $p$ によって決まるというものです。

$Pr(D_{ij} = 1) = p$ for all $ij$ such that $i \neq j$

Erdős-Rényi random graphを始めとして、数多くの random graph models が提案されています。それらはネットワークがなぜある特徴 (スケールフリー性など) を持つかを説明する上で非常に有用です。しかし、それらのモデルが欠いているのは、ネットワークが個々人の選択によって形成されるという側面もあるという点です。つまり、ネットワーク形成に伴う個々人のベネフィットとコストを明示的に取り入れる必要が、とりわけ社会ネットワークでは重要となるわけです。例えば、ある人とつながるというイベントは、全くの偶然で引き起こされる点もあれば、何らかの戦略的な意図を持ったものでもありえます。とりわけ、ビジネスにおいては後者のような「ネットワーキング」が鍵となる場面もしばしば起こりえます。こうした個々人のインセンティブを考慮したネットワーク形成のモデリングを戦略的ネットワーク形成モデル (strategic network formation model) と呼びます。

インセンティブを明示的にモデル化するのは、経済学の十八番です。とりわけ、ネットワーク形成は個々人の利得と行動が相互に依存する「戦略的状況」と考えるのが自然です。そうなるとゲーム理論の道具がたくさん使えるように思われます。例えば、AさんとBさんがいて、彼らがリンクを形成するか否かという状況を考えるとき、その戦略的帰結を導出するためには「ナッシュ均衡」、すなわち自分一人が行動を変えても得をしない状況がゲームのプレーヤー全員について成立している戦略の組を与える解概念が使えそうに思われます。しかし、ナッシュ均衡という解概念は戦略的ネットワーク形成を考える上であまり便利ではないことが指摘されています。それを考えてみましょう。

ここで、ゲームのプレーヤーをあるネットワークを構成するノードの集合を $N = \{1, \ldots, n\}$ と書き、ノードの集合 $N$ のもとで考えられうるネットワークの集合を $G(N)$ と表します。そして、あるネットワークのもとで個々のノードの面するベネフィットとコストは効用関数を用いて $u_{i}: G(N) \rightarrow \mathbb{R}$ と表現します。つまり、 $u_i(g)$ とは、ノード $i$ がネットワーク $g$ のもとで得られる効用を表します。

これを (完全情報同時手番) ゲームとして記述するには、あと1つ、個々人の取りうる戦略空間が必要となります。ここでそうした戦略集合の1つとして、個々があるノードとリンクを形成したいか否かを同時にアナウンスするケースを考えてみます。単純のため、プレーヤーをAとBだけに絞りましょう。AさんとBさんの初期状態としてリンクは形成されていないとします。そして、リンクが形成された場合はお互い正の利得を得られますが、そうでない場合は何も得られないとします。するとこのゲームは以下のような利得表で表現できます。

Aさん \ Bさん	リンクを形成したいと言う	言わない
リンクを形成したいと言う	(1, 1)	(0, 0)
言わない	(0, 0)	(0, 0)

このとき、ナッシュ均衡、つまり自分ひとりが行動を変えても得をしない状態がA、Bさん両名に成り立つ戦略の組が2つ存在します。それは、両方ともリンクを形成したいと言う戦略と、両方ともリンクを形成したいと言わない場合です。前者はまだしも、後者のナッシュ均衡は現実問題を紐解く上ではあまり有用には思えません。最初リンクを形成しないと明言したとしても、そのあとコミュニケーションを重ねることで、両者が同意してリンクを形成することが往々にしてあるからです。上のケースでは、こうしたコミュニケーションや協調に伴うリンク形成が捨象されてしまいます。

逆にAさんとBさんがリンクを既に形成しているケースを考え、そのリンクが切られるケースを考えてみます。リンクを形成する場合は基本的に相互の同意が必要ですが、リンクを切るケースは片一方の意思によって行われるケースが多いです。そういったリンク形成と解消の非対称性をどう表現するかについても考える必要がありそうです。

Pairwise stability

上で見たように、戦略的ネットワーク形成においてナッシュ均衡ではない別の均衡概念があると良さそうです。そこでJackson and Wolinsky (1996) が提案したのが pairwise stability という均衡概念です。あるネットワーク $g$ が pairwise stable であるとは、以下の1、2を両方満たすときのことを言います。

For all $ij \in g$ , $u_i(g) \geq u_i(g - ij)$ and $u_j(g) \geq u_j(g - ij)$
For all $ij \notin g$ , if $u_i(g + ij) > u_i(g)$ then $u_j(g) > u_j(g + ij)$

$ij \in g$ とは、ネットワーク $g$ にエッジ $ij$ が存在することを、 $ij \notin g$ は存在しないことをそれぞれ表します。また、 $ij \in g + ij$ はネットワーク $g$ にエッジ $ij$ を加えたもの、 $ij \in g - ij$ は削除したものをそれぞれ表します。pairwise stabilityとは人間の言葉で言うと、1.ネットワーク上のどのペアも今あるリンクを切りたくない、2.どのペアもこれ以上リンクを形成したくない、と言い換えることができます。1つ目の式は $i$ と $j$ の両方がリンクを維持したい思わないとリンク $ij$ は維持されないということを意味しますから、リンクの切断は片一方の意思によって行われてもよいことを含意しています。逆に2つ目の定義は、 $i$ と $j$ の両方が得をしないとリンクが形成されないことから、両者の同意が無いとリンクが形成されないことを含意しています。このように、pairwise stability という概念は片一方の意思による一方的なリンクの切断と、リンク形成におけるコミュニーケーションや協調という側面を暗黙的に取り入れています。この概念は、戦略的ネットワーク形成におけるナッシュ均衡的な均衡概念として幅広く使われています。

ただしこの pairwise stability というのは、ある時点で1つのリンクの変化しか考慮しないという点で比較的弱い均衡概念となっています。例えば、あるプレーヤーにとっては、リンクを1つだけ切る場合は得をしないが、複数のリンクを一度に切る場合は得になるケースというのも存在し得るでしょう。加えて、pairwise stabilityはネットワークの各ペアごとに関する均衡概念ですが、時にはペア単位ではなくグループ単位で考えることが有用であることもあるでしょう。こうしたケースは pairwise stability では捕捉することができず、より強い均衡概念が必要となります。その詳細については Jackson (2008) を参照ください。私も目下勉強中です。

この pairwise stability を導入すれば、先程考えたAさんとBさんによるリンク形成ゲームでは、AさんとBさんがリンクを形成したネットワークのみが pairwise stability と適合します。

Pairwise stability does not necessarily imply efficiency

pairwise stability は、リンクを新たに作りたくないし消したくもないという意味で、ネットワーク上の個々のペアにとって最適なネットワークを明らかにする均衡概念でした。ただし、そのネットワークが社会的に望ましいものかどうかは明らかではありません。加えて、pairwise stable なネットワークは一般に複数存在するため、どのネットワークが他と比べて望ましいかを判断する指標が欲しくなります。そこでその「望ましさ」を評価するために、ネットワークの各プレーヤーに対して定めた効用関数を用いて、以下の2つの概念を導入します。

あるネットワーク $g$ がパレート効率的 (Pareto efficient) であるとは、全ての $i$ に対して $u_j(g') \geq u_j(g)$ が成り立ち、かつある $i$ に対して $u_j(g') > u_j(g)$ となるようなネットワーク $g' \in G(N)$ が存在しないようなことを言う。
あるネットワーク $g$ が効率的 (efficient) であるとは、すべての $g' \in G(N)$ に対して $\sum_i u_i(g) \geq \sum_i u_i(g')$ が成り立つようなことを言う。

ある人の効用をあげようとすると、別の人の効用を犠牲にしなければならない状態という意味で効率的だというのが前者、効用の総和を最大化するようなネットワークが効率的であるというのが後者です。これらの「望ましさ」の指標は、Erdős-Rényi を始めとする random garph model にはなかったもので、ノードの効用を導入することで考えることが可能となったものです。私たちはネットワークを評価する新たな見方を獲得することができたわけです。

一般に pairwise stable なネットワークは (Pareto) efficient とは必ずしもありません。それを考えるために、Jackson and Wolinsky (1996) の connection model を考えてみましょう。つまり、

直接のつながりからは benefit として $\delta$ ( $0 \lt \delta \lt 1$ )を得るが、cost として $c$ がかかる。
間接的なつながりからも benefit を得るが、その benefit の大きさはつながりの距離 $d$ ( $d \geq 2$ )とすると $\delta^{d}$ となる。すなわち、つながりが遠くなるほどその benefit は減衰する。間接的なつながりによるコストは発生しない。

という単純なモデルを考えます。このとき、以下が成り立ちます。

Proposition (Jackson and Wolinsky, 1996)

$c \lt \delta - \delta^2$ のとき、完全グラフ (任意の2つのノード間がつながっている) のみが効率的である。
$\delta - \delta^2 \lt c \lt \delta + ((n-2)/2) \delta^2$ のとき、すべてのノードによって形成されたスターのみが効率的である。
$\delta + (n-2)/2) \delta^2 \lt c$ のとき、誰ともつながりのないグラフのみが効率的である。

なおスターとは、図のようなただ1つの頂点とそれにつながる「葉」のみを持つグラフのことです。 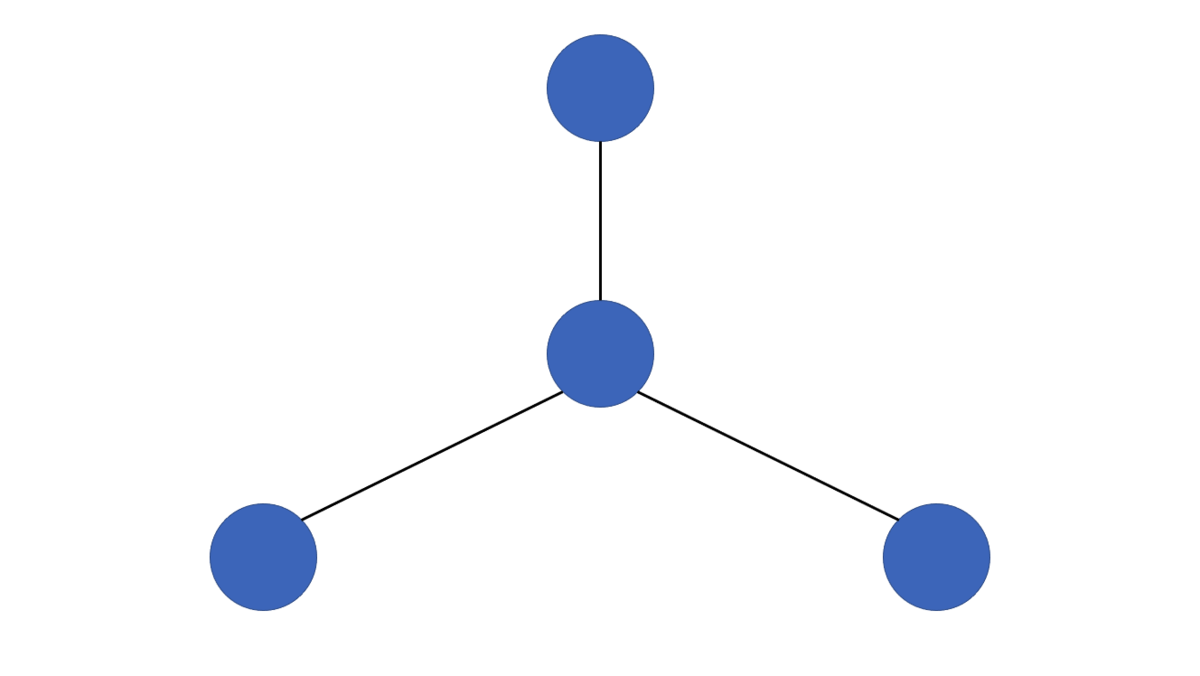f:id:komatsuna4747:20210324215822p:plain 証明は Jackson and Wolinsky (1996) を見ていただくとして、ここではその直感的な意味を確認します。まず 1 のケースは条件式を変えると

$\delta^2 \lt \delta - c$

となり、左辺は間接的なつながり (友達の友達) によって、右辺は直接的なつながりによってそれぞれ得られる効用となります。つまり、友達の友達でいるよりかは、直接つながった方が得をする状態が成立しています。つながりが増えるほど効用の和も単調に増えるわけですから、完全グラフとなったときに効率的となります。

3番目のケースは、人とつながるコストがあまりにも高くなり、つながりが発生すると損をするケースにあたるため、つながりが存在しないグラフが効率的となります。

2番目はそれらの中間、すなわちつながりによるコストがほどほどであるケースです。そのときにスターが効率的になる理由を簡単な例で見てみましょう。

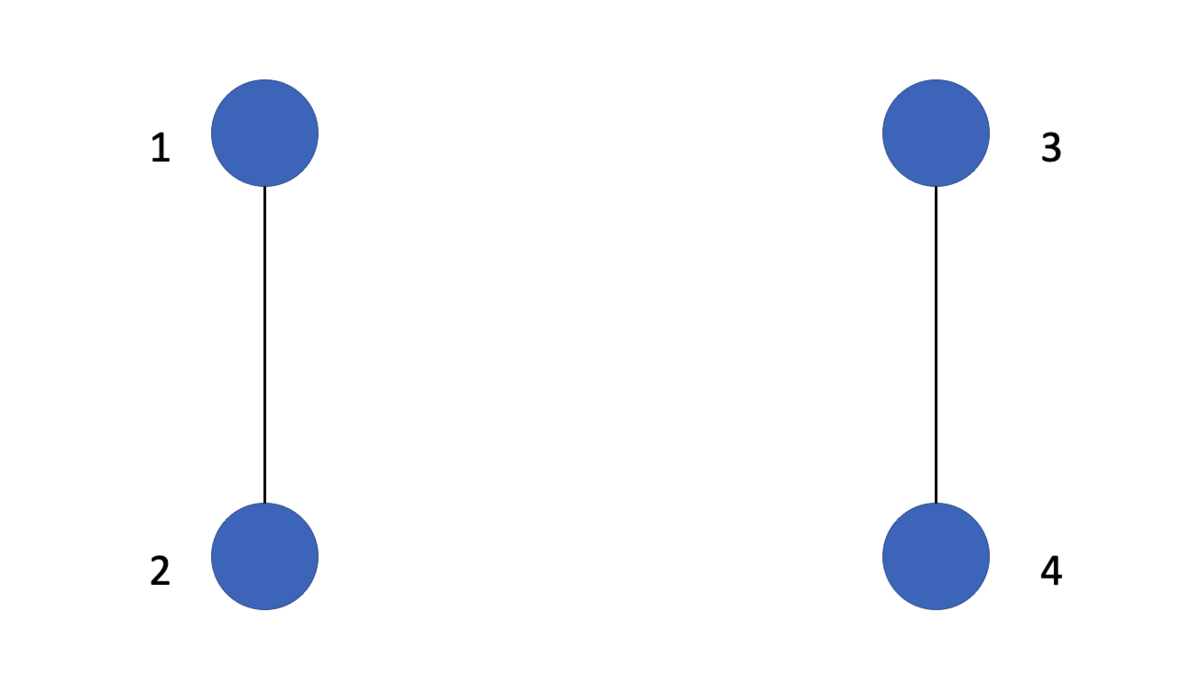
f:id:komatsuna4747:20210324221130p:plain

上の図の、ノード1とノード2、ノード3とノード4が別々につながっているケースを考えてみます。 $u_1 = u_2 =u_3 =u_4 =\delta - c$ ですから、ノードの効用の和は

$W_1 = 4\delta - 4c$

となります。ここで、ノード3とノード4がつながるかわりに、ノード1とノード4がつながるようなスターを考えてみましょう。

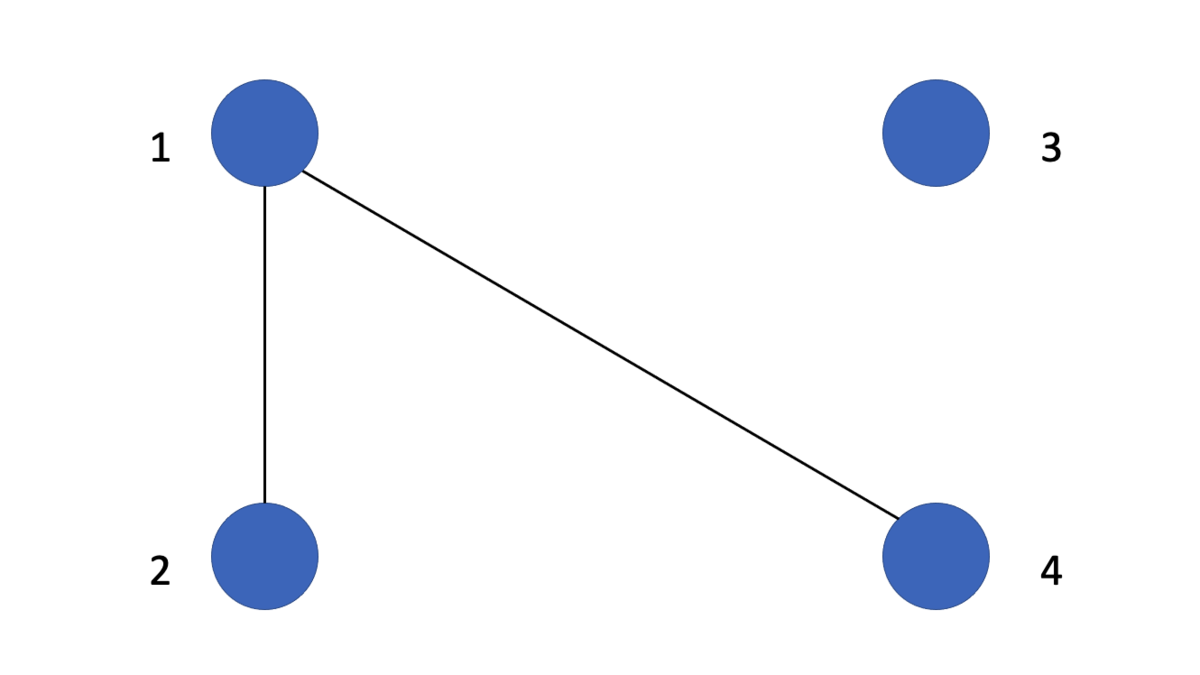
f:id:komatsuna4747:20210324221653p:plain

$u_1 = 2\delta - 2c$ 、 $u_2 = u_4 = \delta - c + \delta^2$ 、 $u_3 = 0$ ですから、効用の和は

$W_2 = 4\delta + 2\delta^2 - 4c$

となります。 $2\delta^2$ が存在する分、 $W_2 > W_1$ となります。別々につながっているよりかは、スターとなった方が効率性の観点からは望ましいわけです。

次に、以下のグラフを考えてみましょう。

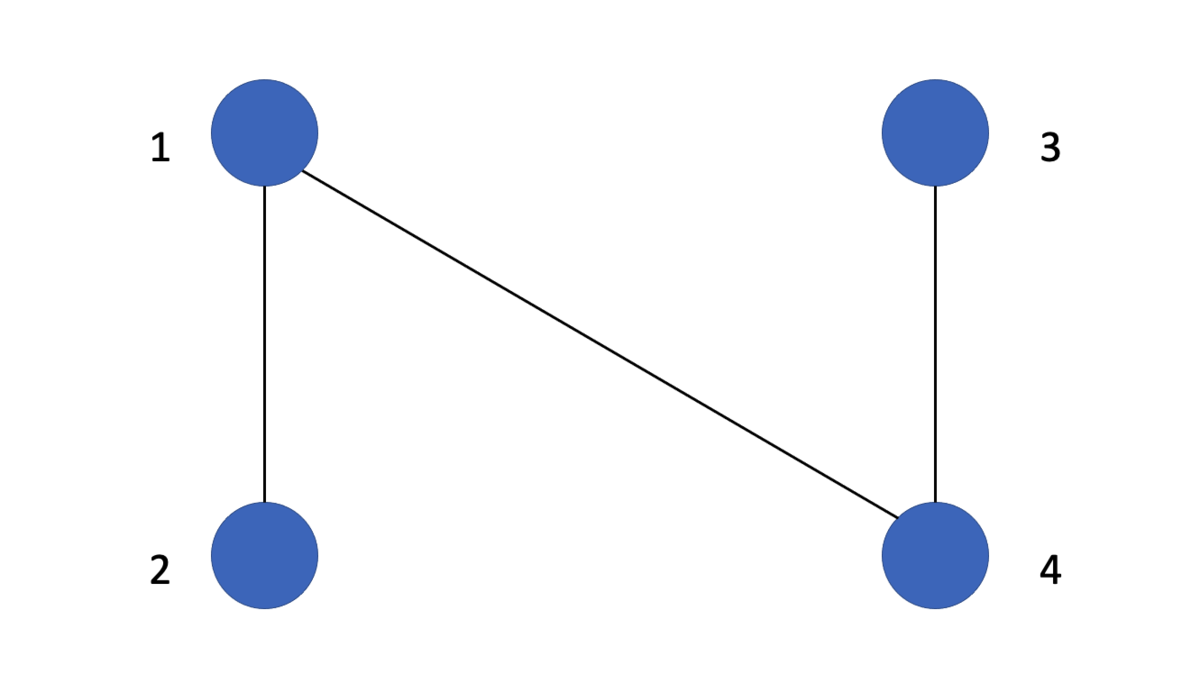
f:id:komatsuna4747:20210324223103p:plain

このとき、 $u_1 = u_4 = 2\delta - 2c + \delta^2$ 、 $u_2 = u_3 = \delta - c + \delta^2 + \delta^3$ なので、効用の和は

$W_3 = 6\delta + 4\delta^2 + 2\delta^3- 6c$

となります。一方、

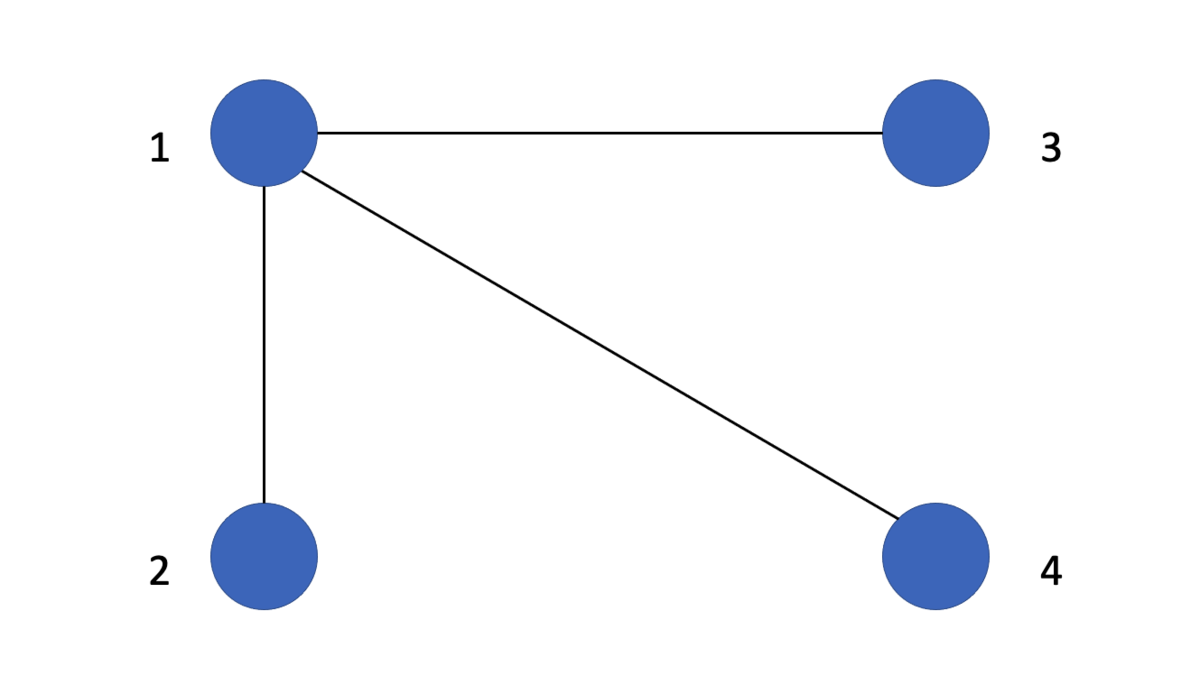
f:id:komatsuna4747:20210324223244p:plain

このようなスターを考えると、 $u_1 = 3\delta - 3c$ 、 $u_2 = u_3 = u_4 = \delta - c + 2 \delta^2$ となるので、効用の和は

$W_4 = 6\delta + 6\delta^2 - 6c$

となります。 $\delta^2 > \delta^3$ ですから、直感的に $W_4 > W_3$ が成り立ちそうです (実際2の条件下で成立します)。同様にして、完全グラフよりもスターの方が効用の和が高いことが示されます。人間の言葉でいうと、つながりのコストがほどほどにある場合は、直接的なつながりと間接的なつながりがほどほどのバランスで存在する状態が望ましく、かつ遠いつながりを生まないようにすることが効率性を達成する上で大事なようです。それらを満たすグラフがスターであるというわけです。つながりのコストがほどほど存在するときには、誰かハブとなるような人間を置いて、その人を介した方が良いというわけですね。

これまで効率性という観点からネットワークを眺めていましたが、では pairwise stability の観点から見るとどうなるのでしょうか。上で述べた Jackson and Wolinsky (1996) の Proposition のうち、1のケースでは完全グラフが、3のケースでは空のグラフがそれぞれ pairwise stable であることがわかります。pairwise stability の定義に当てはめてみれば、1のケースは誰もリンクを切るインセンティブが、3のケースは誰もリンクを形成するインセンティブがそれぞれないというのはわかると思います。したがってこれらのケースでは pairwise stable network = efficient network となります。

問題はスターのケースです。再び以下のスターに登場いただきましょう。

f:id:komatsuna4747:20210324223244p:plain

このとき、スターの中心であるノード1の効用は $u_1 = 3\delta - 3c$ でした。もしコストが $\delta \lt c \lt \delta + \delta^2$ を満たすとすると、 $u_1 \lt 0$ となりますから、ノード1は全てのリンクを切ることが合理的となります。つまりこのスターは pairwise stable ではありません。しかし $\delta \lt c \lt \delta + \delta^2$ のとき、上の Proposition の2の条件を満たしていますから、全てのノードがつながったスターが効率的なわけです。したがって、pairwise stable network ≠ efficient network となります。

この非効率性はどこから来るのでしょうか。このスターのケースでは、効用の和は

$6\delta + 6\delta^2 - 6c$

です。一方、ノード1の効用は

$u_1 = 3\delta - 3c$

でした。両者を比べると、ノード1の効用には、間接的なつながりから得られる benefit である $\delta^2$ の項が含まれていません。ノード2、ノード3、ノード4はこの間接的なつながりの恩恵を受けているわけですが、ノード1の意思決定には、こうした間接的なつながりの benefit は考慮に入れられていません。これが非効率性の原因となっているわけです。

以上 connection model を見てわかったように、efficiency と pairwise stability の間に生まれる conflict の要因として、外部性 (externality) の存在が挙げられます。その定義を書いておきましょう。

ある効用関数の組 $u = (u_1, \ldots, u_n)$ のもとで非負の外部性 (non-negative externality) が存在するとは、全ての $i \neq j \neq k$ となるような $i \in N$ 、 $g \in G(N)$ 、 $jk$ に対して $u_i(g + jk) \geq u_i(g)$ が成り立つことである。 (非正の外部性 (non-positive externality) は不等号が逆のケースのことを指す)。

このように当事者以外の存在が当事者同士の関係に間接的に効くケースは、現実世界でも多々あるでしょう。例えば、AさんがBさんと初対面で話をしていると、共通の友人Cさんがいることに気づき、その共通の友人をきっかけに話が弾んだりすることもあるかと思います。その意味で、AさんとBさんの効用には、共通の友人であるCさんの存在に影響を受けているはずです。問題は、AさんとBさんがリンクを形成する意思決定を行う際に、Cさんを介した間接的なつながりから得られるベネフィットが、AさんBさんの間だけでなくネットワーク全体にとっても望ましいことを考慮に入れていない点です。つまり、正の外部性が存在するとき、社会的限界便益と私的限界便益が一致しないことによる非効率が発生してしまうわけです。先程の connection model における非効率性もこのケースにあたります。

外部性による非効率性が発生するということは、政府による介入が妥当性を持ちうるケースとなります。学部のミクロ経済学で学んだことを思い出すと、例えばつながりに対して補助金/税をかけて、外部性を内部化することが一つの解決手段だったかと思います。また Coase の定理が教えてくれることは、取引コストが存在しないならば、当事者同士の交渉により何らかの transfer が達成されることで効率的な資源配分が達成できるということでした。こうした transfer を明示的に取り入れると、プレーヤー $i$ の効用は $u_i(g) + t_i(g)$ と書けるでしょう。ただし $t_i(g)$ はプレーヤー $i$ がネットワーク $g$ の元で受け取る/支払う transfer です。特に各ペア同士で transfer し合う状況を考えたときの pairwise stability を、pairwise stability with transfers と呼び、以下の2つを満たすときのことをいいます。

$ij \in g$ ならば、 $u_i(g) + u_j(g) \geq u_i(g - ij) + u_j(g-ij)$ が成り立つ。
$ij \notin g$ ならば、 $u_i(g) + u_j(g) \geq u_i(g + ij) + u_j(g + ij)$ が成り立つ。

$i$ と $j$ の間の transfer を考えるので、上の定義ではその transfer は相殺され消えています。

ところが、こうした transfer を考えたとしても、efficient なネットワークを必ずしも達成できるとは限らないことが知られています (Jackson and Wolinsky, 1996)。コースの定理を前提とすると、交渉による transfer によって efficient なネットワークを達成できそうです。しかし Jackson and Wolinsky (1996) によると、直感的には複数の外部性を一度に考慮しなければならない点が問題を複雑にしているようです。また勉強しておきます。

終わりに

以上簡単ではありますが、ネットワーク形成過程における代表的な均衡概念である pairwise stability と、外部性という概念を見ました。これらの概念をもとにして、実際にどのように計量モデルへと接合していくかを、Mele (2017) を例として次回以降見ていきたいと思います。ネットワーク形成モデルの推定を難しくしているのは間違いなく外部性の存在であり、それを推定するために ERGM なる統計モデルをわざわざ使用する研究が多いわけです。

Mele (2017) では、ネットワーク形成ゲームを potential game というクラスを用いて表現しています。potential game なるものを導入する意義や、そこからどう計量モデルに接合していくかを見ていけたらと思っています。

References

Banerjee, A., Chandrasekhar, A. G., Duflo, E., & Jackson, M. O. (2013). The diffusion of microfinance. Science, 341(6144).
Calvó-Armengol, A., Patacchini, E., & Zenou, Y. (2009). Peer effects and social networks in education. The Review of Economic Studies, 76(4), 1239-1267.
Conley, T. G., & Udry, C. R. (2010). Learning about a new technology: Pineapple in Ghana. American economic review, 100(1), 35-69.
De Paula, Á. (2020). Econometric models of network formation. Annual Review of Economics, 12, 775-799.
Graham, B. (2020). Network data. Handbook of econometrics, 7A, 111-218.
Jackson, M. O., & Wolinsky, A. (1996). A strategic model of social and economic networks. Journal of economic theory, 71(1), 44-74.
Jackson, M. O. (2010). Social and economic networks. Princeton university press.
Mele, A. (2017). A structural model of dense network formation. Econometrica, 85(3), 825-850.
Nakajima, R. (2007). Measuring peer effects on youth smoking behaviour. The Review of Economic Studies, 74(3), 897-935.
Topa, G. (2001). Social interactions, local spillovers and unemployment. The Review of Economic Studies, 68(2), 261-295.

buildersbox.corp-sansan.com