f:id:komatsuna4747:20210127160740j:plain

Sansan R&D 研究員の小松です。ERGMの性質についてこれまで眺めています。前回の記事では以下を確認しました。

ERGM から生成されるネットワークの構造は、パラメーターが変わると極端に変化する(相転移)。
パラメーターの値が相転移の境界線にあるとき、ネットワークの分布は二峰性を示す。このとき、リンクを各ステップで1つずつアップデートするようにしてネットワークをシミュレーションすると、シードとなるネットワークによっては正しくないネットワークに収束することがある。

本稿では、Mele (2017) が提案した large sampler を実装し、それがネットワークの分布が二峰性を示すときにネットワークの収束を改善するのかを確認します。

Trapped in local maxima

前回見た例では、edges, triangles のパラメーターがそれぞれ $(\alpha, \beta) = (1, -1)$ であるとき、ネットワークの統計量の分布は二峰性を示すのでした。それは、Chatterjee and Diaconis (2013) の Theorem 4.2 に基づけば、 $n$ が十分大きくかつ $\beta$ が非負であるとき、定常分布におけるネットワークの density は

$u^{*}(\alpha, \beta) := \arg \max_{0 \leq u \leq 1} \left( \alpha u + \beta u^3 - \frac{1}{2} u \log u - \frac{1}{2} (1 - u) \log (1 - u)\right)$

によって与えられ、 $(\alpha, \beta) = (1, -1)$ のとき $u^{*}(\alpha, \beta)$ は以下のように $u$ が 1 に近い部分で local maxima を持つからです。

f:id:komatsuna4747:20211114134512p:plain

このようにネットワークの統計量が二峰性を示すとき、リンクを1つずつアップデートする方法では、定常分布に収束するまでには指数時間かかることが示されています (Bhamidi et al., 2011; Mele, 2017)。つまり一度 local maxima にとらわれてしまうと、そこから抜け出すことは困難になります。その状況が、下図の真ん中のケースにあたります。

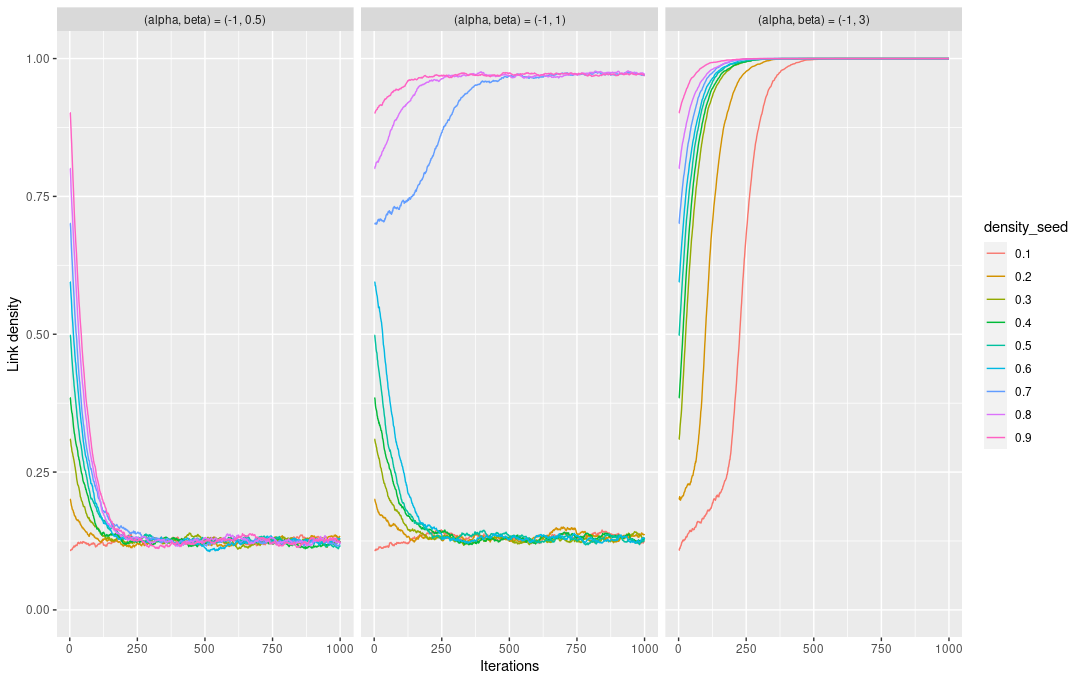
f:id:komatsuna4747:20210908020623p:plain

Getting out of local maxima

パラメーターの値によっては local maxima にトラップされてしまうことがわかったわけですが、そこから抜け出すにはどうすればよいのでしょうか。そこで Mele (2017) では、1回のステップで複数のリンクを同時にアップデートする large sampler を提案しました。具体的には、リンクをアップデートする各ステップで、一定の確率で以下の操作のうちどれかを行います。

あるノード1つをランダムに選び、そのノードのもつリンクをすべて切り、つながっていないペアについてはリンクを作成する。
複数のペアをランダムに選択し、それらのペアにリンクがなければ作成、リンクがあれば切る。
ネットワーク全体のリンクをフリップする。つまり、ネットワークを adjacency matrix $G$ 、単位行列を $I$ で表現したとき、 $G := I - G$ とする。

この large sampler を導入することで、収束が改善するかを見てみましょう。筆者の Mele が作成した {netnew} パッケージを用いてもよいですが*1、今回は私が ERGM を勉強するために作成した {myergm} を用いて確認してみましょう*2。使用したコードは本記事の末尾に添付しています。

github.com

$(\alpha, \beta) = (1, -1)$ のとき、local sampler と local + large sampler の結果を比較したものが下図です。左の local sampler のみを用いた場合は、ネットワークの初期値によって local maxima に収束していることがわかります。一方、右の large sampler を導入したケースでは、ネットワークの初期値に関わらずすべて同じ density のネットワークに収束していることがわかります。急激にネットワークの状態が変わっていることから、特にネットワーク全体のリンクをフリップすることが、local maxima から抜け出す上で役に立っていることが伺えます。

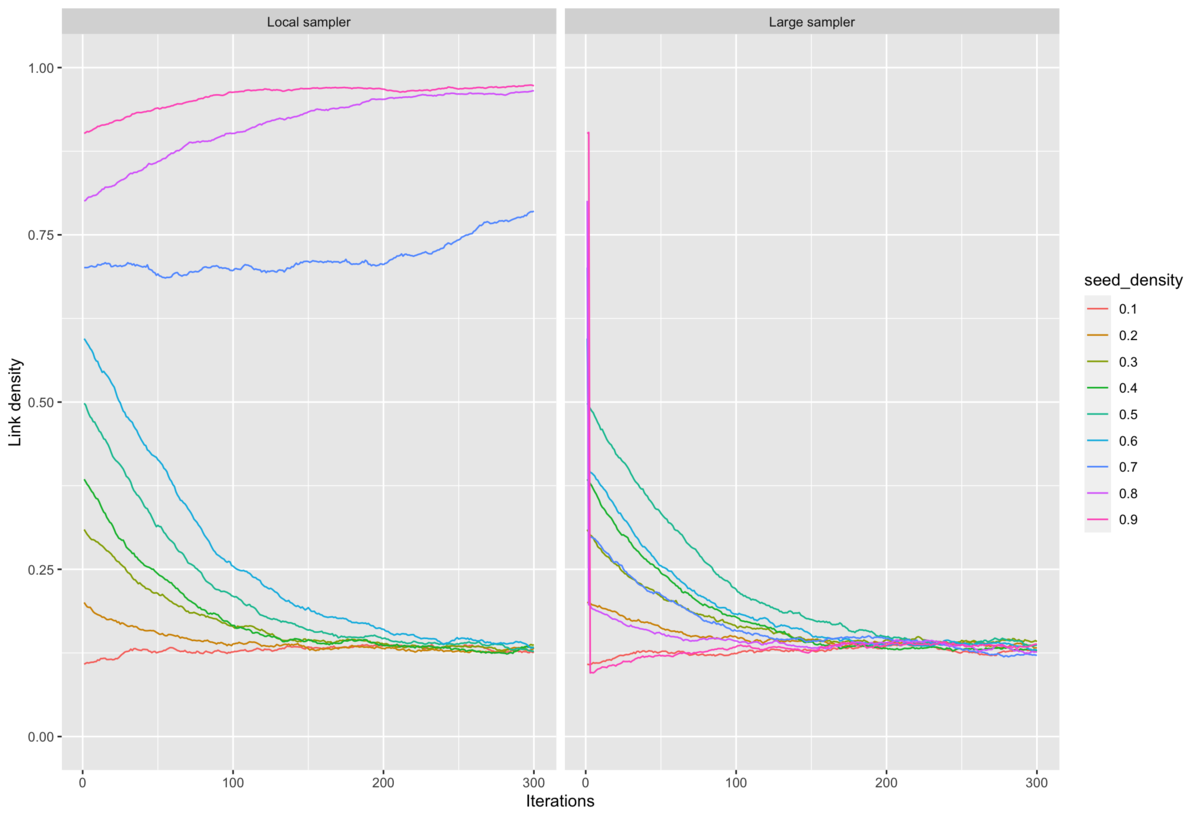
f:id:komatsuna4747:20220213004459p:plain

ただし計算上の注意として、大きなネットワークを対象にシミュレーションを行う場合、large sampler を使用するとメモリにのらない可能性が高いです。というのも、adjacency matrix $G$ が sparse であっても、 $I - G$ は dense (non-zero elements が非常に多くなる) ためです。サンプルコードで遊ぶ場合は、 $N$ の大きさに注意してください。

Why convergence is important

これまでネットワークをシミュレーションする際に発生する問題、およびその解決方法の1つについて議論してきました。なぜこれらが重要かというと、効用関数のパラメーターを推定するために、ネットワークをMCMCでシミュレーションする必要があるからです。

ERGM の難しさを思い出すと、尤度関数の分母 (normalizing constant) の計算が現実的な時間であるため、最尤法など通常の推定手法が使えない点にありました。そこで、ERGM のパラメーターを固定した上でネットワークをMCMCを作成し、そこからサンプリングされたネットワークを用いてパラメーターを推定する方法が使われています。そのネットワークのシミュレーションがうまくいかない (収束しない) と、当然パラメーターの推定もうまくいかないわけです。ということで次回は ERGM のパラメーターを実際に推定するところを眺めたいと思います。

References

Bhamidi, S., G. Bresler, & A. Sly (2011). Mixing Time of Exponential Random Graphs. The Annals of Applied Probability, 21(6), 2146–2170.
Chatterjee, S., & Diaconis, P. (2013). Estimating and understanding exponential random graph models. Annals of Statistics, 41(5), 2428-2461.
Mele, A. (2017). A structural model of dense network formation. Econometrica, 85(3), 825-850.

Sample code

devtools::install_github("komatsuna4747/myergm")

library(ggplot2)
library(magrittr)

# Number of nodes
N <- 100
# Set coefficients
coef_edges <- -1
coef_triangle <- c(0.5, 1, 3)
# Density of seed networks
density <- seq(0.1, 0.9, by = 0.1)
# Generate Erdos-Renyi networks for different densities
list_seed_network <-
  withr::with_seed(
    seed = 334,
    as.list(density) %>%
      purrr::map(
        function(x) {
          net <- network::network(N, density = x, directed = FALSE)
          net <- igraph::get.adjacency(intergraph::asIgraph(net))
          return(net)
        } 
      )
  )

# Coefficients
coef_edges <- -1
coef_triangle <- 1/N

# Simulate networks and calculate sufficient statistics
# Ugly code. There must be better ways to do this.
df <-
  list(0, 0.01) %>%
  purrr::map_df(
    ~purrr::map2_df(
      list_seed_network,
      as.list(density),
      function(x, y) {
        sampler <- ifelse(. == 0, "Local sampler", "Large sampler")
        logger::log_info("Simulating network... density {y}, {sampler}")
        netstat <-
          myergm::create_MCMC(
            adjmat = x,
            coefEdges = 2 * coef_edges,
            coefTriangle = 6 * coef_triangle,
            MCMC_interval = 100,
            MCMC_samplesize = 300,
            MCMC_burnin = 0,
            p_one_node_swap = .,
            p_large_step = .,
            p_invert = .
          )
        logger::log_info("Finished imulating network: density {y}")
        output <- 
          tibble::tibble(
            seed_density = as.character(y),
            sampler = sampler,
            iter = 1:nrow(netstat),
            edges = netstat[, 1],
            triangle = netstat[, 2],
          ) %>%
          dplyr::mutate(density = edges / (N * (N - 1) / 2))
        return(output)
      }
    ) 
  )

g <-
  ggplot(data = df, aes(x = iter, y = density, group = seed_seed, color = seed_density)) +
  geom_line() +
  ylim(0, 1) +
  xlab("Iterations") +
  ylab("Link density") +
  facet_grid(~ sampler)
plot(g)