f:id:komatsuna4747:20210127160740j:plain

Sansan DSOC R&D 研究員の小松です。前回は、R で ERGM を扱うことに慣れることから始め、ERGM に関わる問題点をあげていきました。

そこであげた問題点は以下の通りでした。

難点その1: リンク間の相互依存関係を考慮する時、ERGM の尤度関数の分母が現実的な時間内に計算不可能である。

難点その2: ERGM から生成されるネットワークの構造は、パラメーターが変わると極端に変化する。

難点その3: 外部性のパラメーターが全て非負であるとき、それらを識別することはできない。

今回は、2点目と3点目に関する理論的な結果を示した Chatterjee and Diaconis (2013) の結果を眺めることにしましょう。

Model

これまでの連載と同様、ノード数が $n$ のループのない、undirected なグラフ $G = [g_{ij}$ ] を考えます。ここで、各個人がだれとつながるかを考えるときに、直接のつながりと、共通の友人の存在によって影響を受けるとします。このようなネットワーク形成モデルの一例として、以下が考えられます。

$\begin{align} p_{i}(G; \alpha, \beta) = \exp\left(2\alpha \sum_{i=1}^{n} \sum_{j=1}^{n} g_{ij} + \frac{6\beta}{n} \sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{j=1}^{n} g_{ij} g_{jk} g_{ki} - n^2 \psi_{n}(\alpha, \beta) \right) \end{align}$

$\sum_{i=1}^{n} \sum_{j=1}^{n} g_{ij} =: E(G)$ はエッジの数、 $\sum_{j=1}^{n} \sum_{j=1}^{n} g_{ij} g_{jk} g_{ki} := \Delta(G)$ は三角形の数、 $\psi_{n}(\alpha, \beta) := \frac{1}{n^2} \log \sum_{g' \in \mathcal{G}_{n}} \exp(2\alpha E(g') + \frac{6\beta}{n} \Delta(g'))$ は正規化定数 (つまり、 $p_{i}(G; \alpha, \beta)$ を $G$ についてすべて足し合わせると1になるように調整するための定数) です。この正規化定数はノード数 $n$ のときに考えられるグラフの集合 $\mathcal{G}_{n}$ の要素の数があまりにも大きいため、現実的な時間で計算することができません。

Main results

しかし、 Chatterjee and Diaconis (2013) の Theorem 3.1 と 4.1 によると、 $n$ が十分大きくかつ $\beta$ が非負であるとき、正規化定数 $\psi_{n}(\alpha, \beta)$ は以下のように近似できます。

$\begin{align} \psi_{n}(\alpha, \beta) \approx \sup_{0 \leq u \leq 1} \left( \alpha u + \beta u^3 - \frac{1}{2} u \log u - \frac{1}{2} (1 - u) \log (1 - u) \right) \end{align}$

この右辺の最大値を与える $u$ を $u^{*}(\alpha, \beta)$ とおきます。 Chatterjee and Diaconis (2013) の Theorem 4.2 は、任意の $\alpha \in \mathbb{R}$ と $\beta > 0$ に対して、 $p_{i}(\cdot ; \alpha, \beta)$ から発生させたグラフと、各エッジを確率 $u^{*}(\alpha, \beta)$ で独立に発生させた Erdos–Renyi グラフと本質的には変わらないことを示しました。これは、先述した「難点その3: 外部性のパラメーターが全て非負であるとき、それらを識別することはできない」に対応します。共通の友人がつながりに影響を与える効果である $\beta$ が非負であるとき、その識別はできないというわけです。つまり、 $u^{*}(\alpha, \beta)$ とある関係式をみたす $\alpha$ を $\alpha '$ としたとき、 $p_{i}(\cdot ; \alpha, \beta)$ から発生させたグラフと $p_{i}(\cdot ; \alpha ', 0)$ から発生させたグラフは区別がつきません。

共通の友人の影響を識別できないのは残念です。一方そうしたネットワークをシミュレーションするときは、リンクの相互依存関係を考慮した複雑な計算を行う必要はなく、 $u^{*}(\alpha, \beta)$ を計算し、ネットワークの各ペアのリンクを確率 $u^{*}(\alpha, \beta)$ で発生させればよいことになります。

今考えているモデルはどのようなネットワークを生成し、そしてパラメーターが $\alpha \in \mathbb{R}$ と $\beta > 0$ を動くとき、そのネットワークの構造はどう変わるのでしょうか。これを見るために $u^{*}(\alpha, \beta)$ を計算し、その contour plot を描いたものが以下です。

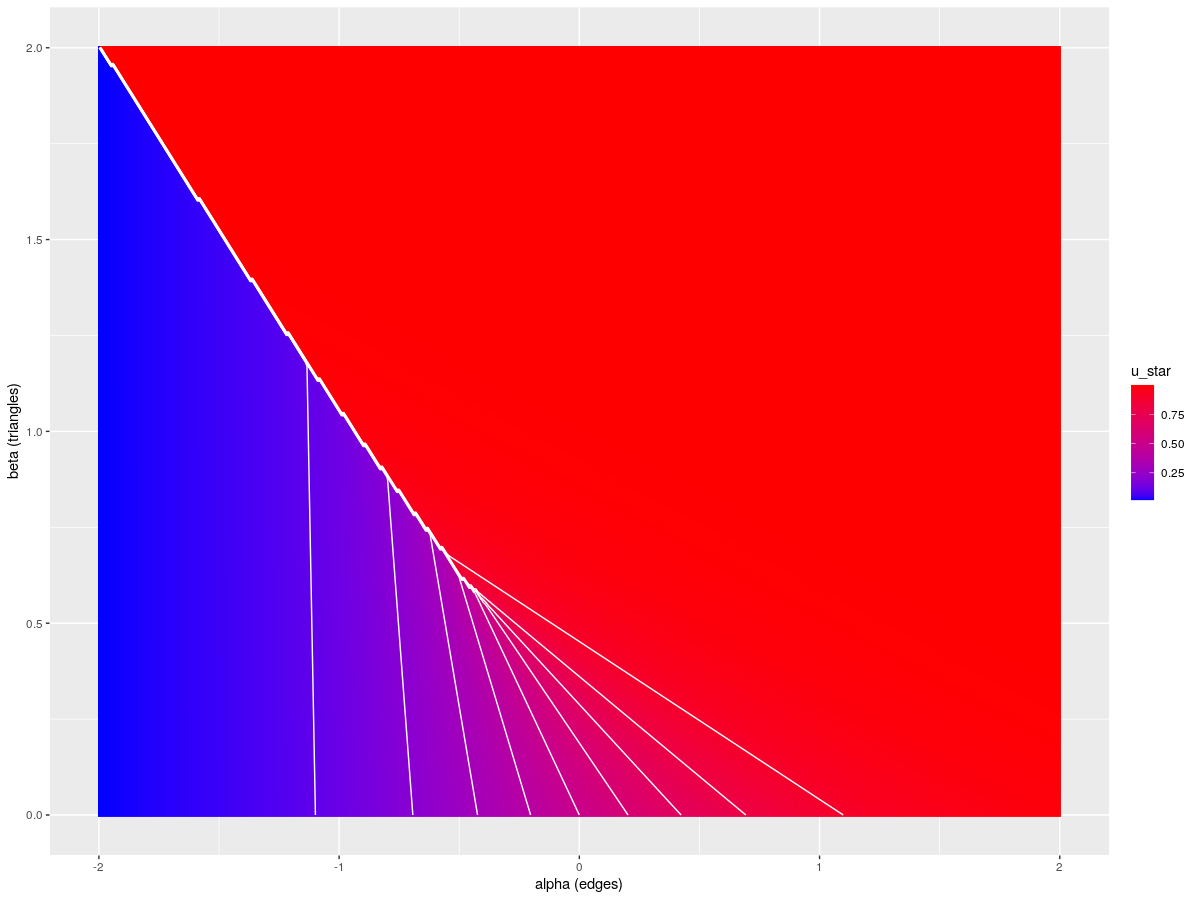
f:id:komatsuna4747:20211101000225p:plain

$u^{*}(\alpha, \beta)$ はグラフの密度とほぼ等しく、青い領域では密度の低いグラフ、赤い領域では密度の高いグラフがそれぞれ生成されます。このグラフは以下の R のコードで簡単に作成できます。

library(ggplot2)
library(magrittr)

psi <- function(u, beta1, beta2) {
  output <- beta1 * u + beta2 * u^3 - (u * log(u))/2 - ((1 - u) * log(1 - u))/2
  return(output)
}

u_star <- function(beta1, beta2) {
  init_par <- list(0.1, 0.9)
  result <- 
    init_par %>%
    purrr::map(
      function(x) {
        optim(par = x, fn = psi, beta1 = beta1, beta2 = beta2, lower = 0.0001, upper = 0.9999, control = list(fnscale = -1), method = "L-BFGS-B")
      }
    )
  output <- ifelse(result[[1]]$value >= result[[2]]$value, result[[1]]$par, result[[2]]$par)
  return(output)
}

params <-
  list(param_edges = seq(-2, 2, by = 0.01), param_triangle = seq(0, 2, by = 0.01)) %>%
  purrr::cross_df()

params %<>%
  dplyr::mutate(
    u_star = unlist(purrr::map2(as.list(param_edges), as.list(param_triangle), u_star))
  )

g <-
  ggplot(data = params, aes(x = param_edges, y = param_triangle, z = u_star)) +
  geom_raster(aes(fill = u_star)) +
  scale_fill_gradientn(colors = c("blue", "red")) +
  geom_contour(color = "white") +
  xlab("alpha (edges)") +
  ylab("beta (triangles)")

plot(g)

ここで注目すべきは、図の左上の領域では境界線によって赤い領域と青い領域がはっきりと分かれている点です。その境界線の周辺では、 $(\alpha, \beta)$ の値が少し変わると生成されるグラフが極端に変化することが示唆されます。これが、冒頭に述べた難点のうち、「難点その2: ERGM から生成されるネットワークの構造は、パラメーターが変わると極端に変化する」に対応するわけです。こうした現象は 相転移 (phase transition) と呼ばれます。

パラメーターの値がこの相転移がおこる境界線にあるとき、ネットワークの統計量の分布は二峰性 (bimodal) を示します。Chatterjee and Diaconis (2013) の Theorem 4.2 に基づけば、 $n$ が十分大きくかつ $\beta$ が非負であるとき、ネットワークの density は

$\begin{align} u^{*}(\alpha, \beta) :=\arg \max_{0 \leq u \leq 1} \left( \alpha u + \beta u^3 - \frac{1}{2} u \log u - \frac{1}{2} (1 - u) \log (1 - u) \right) \end{align}$

と $u^{*}(\alpha, \beta)$ を見ればわかるのでした。上の図で $(\alpha, \beta) = (-1, 1)$ が相転移の境界線の近くにあります。このとき $\alpha u + \beta u^3 - \frac{1}{2} u \log u - \frac{1}{2} (1 - u) \log (1 - u)$ がどのような関数になっているかを図示したものが以下です。

f:id:komatsuna4747:20211114134512p:plain

$u$ の値が 0.125 あたりと、1 に近い部分でそれぞれ極大になっていること、そしてこの関数の最大値は $u$ が 0.125 あたりのときであることがわかります。ここで、前回の記事 (https://buildersbox.corp-sansan.com/entry/2021/09/08/120000) の "Simulating Networks" の部分で、 $(\alpha, \beta) = (-1, 1)$ のとき、シミュレーションを開始する最初のネットワークによって、最終的に収束するネットワークの密度が異なっていたことを思い出します。下の図の真ん中のケースです。

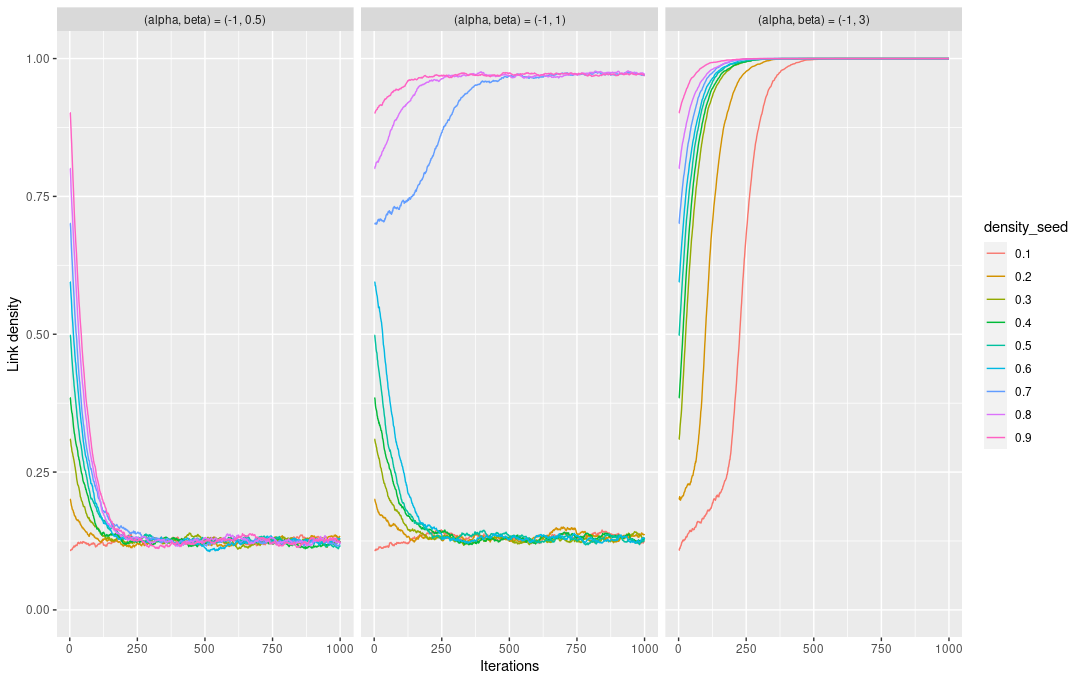
f:id:komatsuna4747:20210908020623p:plain

真ん中の図の上3つのケースは、1に近い部分で収束していることがわかります。この収束先が、先程の関数の local maximum に対応しているわけです。 $(\alpha, \beta) = (-1, 1)$ のときの global maximum は $u$ が 0.125 周辺にあるわけですから、真ん中の図の上3つの線も最終的には 0.125 周辺に収束しなければなりません。上3つのケースは local maximum にトラップされており、正しくネットワークを生成できていないことになります。

このように local maxima にトラップされるのは、ネットワークを MCMC でシミュレーションするときに、各ステップでリンクを1つずつアップデートするような local sampler を採用していることに起因します。local maxima に一旦引っかかってしまうと、local sampler ではそこから抜け出すことが困難であるわけです。その対処法の1つとして Mele (2017) が提案したものが、1つのステップで複数のリンクを同時にアップデートする global sampler です。このあたりの話は、シミュレーション・パラメーターの推定の詳細含めて次回で議論します。

以上まとめると、

ネットワークが直接のつながりと共通の友人の影響によってその形状が決まり、かつ共通の友人の影響がつながりに正に効くときは、パラメーターの値によって生成されるネットワークの形状が大きく変化する (相転移)。
パラメーターの値が相転移の境界線にあるとき、ネットワークの分布は二峰性を示す。このとき、リンクを各ステップで1つずつアップデートするようにしてネットワークをシミュレーションすると、シードとなるネットワークによっては正しくないネットワークに収束することがある。

となります。

References

Chatterjee, S., & Diaconis, P. (2013). Estimating and understanding exponential random graph models. Annals of Statistics, 41(5), 2428-2461.
Mele, A. (2017). A structural model of dense network formation. Econometrica, 85(3), 825-850.