f:id:komatsuna4747:20210127160740j:plain

Sansan DSOC R&D 研究員の小松です。前回の記事では、ネットワーク形成ゲームが Exponential Random Graph Model (ERGM) に収束する証明を確認しました。 buildersbox.corp-sansan.com

ERGM を推定することで、効用関数のパラメーター (例えば、共通の友人の存在がある人同士のつながりやすさにどの程度影響を与えるか) を推定したり、推定したモデルからネットワークをシミュレーションしたりできます。ところが ERGM は色々と気難しい性質があり、多くの研究者がその性質の解明や改善案を提案しています。

これまでは数式を用いた議論が多かったので、ERGM の詳細は脇に置いておき、実際にコードを用いて ERGM で遊ぶところから始めましょう。

Estimating ERGMs

ERGM は、社会ネットワーク分析の分野で広く活用されている手法です。社会ネットワーク分析の主要ジャーナルである Social Networks では、2000年以降 ERGM を言及する論文数が大きく増加しています (鈴木, 2018)。この背景として、ERGM に関する統計的性質の解明と、その推定を行うためのパッケージの整備が進んだことがあげられます。

ERGM を扱うパッケージの代表例が、統計解析ソフト R で開発された {statnet} です。 github.com

これは、ERGM を推定するためのパッケージ {ergm} だけでなく、ネットワークオブジェクトを扱う {network}、社会ネットワーク分析のパッケージ {sna} などが統合されたパッケージです*1。

ひとまず install.packages("statnet") でインストールし、{ergm} を読み込んでみましょう。

library(ergm)

Loading required package: network

‘network’ 1.17.1 (2021-06-12), part of the Statnet Project
* ‘news(package="network")’ for changes since last version
* ‘citation("network")’ for citation information
* ‘https://statnet.org’ for help, support, and other information


‘ergm’ 4.1.2 (2021-07-26), part of the Statnet Project
* ‘news(package="ergm")’ for changes since last version
* ‘citation("ergm")’ for citation information
* ‘https://statnet.org’ for help, support, and other information

‘ergm’ 4 is a major update that introduces some backwards-incompatible changes. Please type
‘news(package="ergm")’ for a list of major changes.

では、実際に ERGM を推定します。undirected network で、以下のような効用関数を考えます。

$\begin{align} u_{i}(g, \theta) = \alpha \sum_{j=1}^{n} g_{ij} + \beta \sum_{j=1}^{n} \sum_{j=1}^{n} g_{ij} g_{jk} g_{ki} \end{align}$

つまり、ある人の効用がその人と直接つながりの数と、共通の友人の数によって決まるとします。それらの影響を決定するパラメーターである $\alpha, \beta$ を推定したいです。

この効用関数のもとで考えるネットワーク形成ゲームは、一定の仮定のもとで、以下のような定常分布に一意に収束するのでした。

$\begin{align} \pi(g, \theta) = \frac{\exp(Q(g, \theta))}{ \sum_{\omega \in \mathcal{G}} \exp(Q(\omega, \theta))} \end{align}$

ただし、

$\begin{align} Q(g, \theta) := \alpha \sum_{i=1}^{n} \sum_{j=1}^{n} g_{ij} + \frac{2}{3} \beta \sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{k=1}^{n} g_{ij} g_{jk} g_{ki} \end{align}$

はポテンシャル関数です。この尤度関数が ERGM と呼ばれる統計モデルのクラスに属するわけです。

ERGM の推定のために、{ergm} が持つメディチ家の婚姻ネットワーク flomarriage を用います。

data(florentine)
plot(flomarriage)

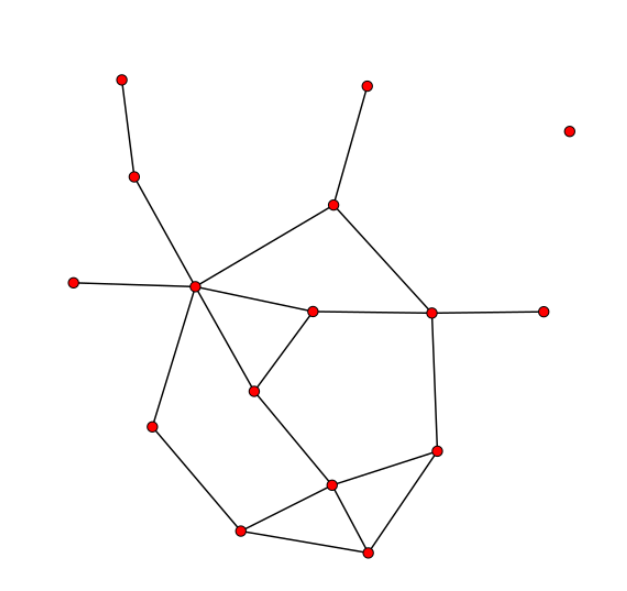
f:id:komatsuna4747:20210906231132p:plain

ネットワークを構成するノードの数は16であり、エッジの数、三角形の数はそれぞれ 20, 3 です。

summary(flomarriage ~ edges + triangle)

   edges triangle 
      20        3

そして今考えるモデルは、以下のコードで簡単に推定することができます。

est_ergm <- ergm(flomarriage ~ edges + triangle, 
                 control = control.ergm(seed = 334)

Starting maximum pseudolikelihood estimation (MPLE):
Evaluating the predictor and response matrix.
Maximizing the pseudolikelihood.
Finished MPLE.
Starting Monte Carlo maximum likelihood estimation (MCMLE):
Iteration 1 of at most 60:
Optimizing with step length 1.0000.
The log-likelihood improved by 0.0017.
Convergence test p-value: < 0.0001. Converged with 99% confidence.
Finished MCMLE.
Evaluating log-likelihood at the estimate. Fitting the dyad-independent submodel...
Bridging between the dyad-independent submodel and the full model...
Setting up bridge sampling...
Using 16 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 .
Bridging finished.
This model was fit using MCMC.  To examine model diagnostics and check for degeneracy, use the mcmc.diagnostics() function.

推定結果を見てみましょう。

summary(est_ergm)

Call:
ergm(formula = flomarriage ~ edges + triangle, control = control.ergm(seed = 334))

Monte Carlo Maximum Likelihood Results:

         Estimate Std. Error MCMC % z value Pr(>|z|)    
edges     -1.6820     0.3510      0  -4.792   <1e-04 ***
triangle   0.1870     0.6068      0   0.308    0.758    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

     Null Deviance: 166.4  on 120  degrees of freedom
 Residual Deviance: 108.1  on 118  degrees of freedom
 
AIC: 112.1  BIC: 117.6  (Smaller is better. MC Std. Err. = 0.0111)

edges, 3/2 * triangle の推定値が、効用関数のそれぞれ $\alpha, \beta$ に対応するわけです。

さて、それっぽい推定結果が出ましたが、本来 ERGM の推定は困難です。

難点その1: リンク間の相互依存関係を考慮する時、ERGM の尤度関数の分母が現実的な時間内に計算不可能である。

ERGM の尤度関数の分母 $\sum_{\omega \in \mathcal{G}} \exp(Q(\omega, \theta))$ は、考えられる全てのネットワークについて和を取ったとき1となるようにするための正規化定数 (normalizing constant) です。この分母そのものが、全てのネットワーク $\omega \in \mathcal{G}$ に対してポテンシャル関数の値 $\exp(Q(\omega, \theta))$ を計算しています。

ここでの問題は、ノード数が $n$ であるとき、考えられるネットワークの組み合わせがいくつ存在するかです。ループの存在しない undirected network を考えたとき、そのネットワーク上で考えられるペアの数は、任意の2つのノードを取ってくる組み合わせの数と等しいので、 $n(n-1)/2$ となります。そしてそのペアそれぞれについて、エッジが張られるか否かを判定すればよいので、考えられるネットワークの数は $2^{n(n-1)/2}$ となります。指数関数が出てきた時点で、嫌な予感がします。考えられるネットワークの集合 $\mathcal{G}$ の大きさは、 $n$ が増えると爆発的に増えてしまうわけです。例えば $n=15$ であったとしても、考えられるネットワークの組み合わせの数は $2^{105} \approx 10^{32}$ と莫大な数になってしまいます。これだけの数だと、 $10^{12}$ 個のポテンシャル関数を計算できるスーパーコンピューターであったとしても、ERGM の尤度関数の正規化定数を計算するためには4,000万年以上かかると言われています (Mele, 2017)。つまり一旦計算が始まってしまうと、それを未来の世代に託さないといけません。

もし、共通の友人の効果が無視できる、つまりネットワークのリンク同士が相互に影響し合う状況でないとき (外部性が存在しない) ときは、上の問題は解消されます。なぜならば、今考える計量モデルが logit と等しくなるからです。しかし、ERGM を用いる大きなベネフィットは、共通の友人の存在のようなリンク間の相互依存関係を明示的に取り込める点にありますから、それを無視することは ERGM を苦労して考える旨味がありません。ERGM の推定を困難にするものは、リンク間の相互依存関係です。

ところが先程の例で {ergm} パッケージを用いて推定したとき、計算時間は 4,000万年もかかっておらず、一瞬で終わりました。ということは、馬鹿正直に尤度関数を計算しているのではなく、何らかの方法でパラメーターの推定を実行可能とするテクニックが使われているようです。それが Markov Chain Monte Carlo (MCMC) simulation methods を用いた方法です (Snijders, 2002)。MCMC を用いてネットワークをシミュレーションすることが、パラメーターを推定の肝となっています。しかし、そのシミュレーションに気難しい点があります。

Simulating networks

与えられたパラメーターから、ERGM はネットワークをシミュレーションすることができます。これによって、推定されたモデルが観察されたネットワークにどの程度 fit しているかを確認したり、counterfactual simulation を行ったりすることが可能となります。数式の詳細は次回以降に譲るとして、ここでも {ergm} を用いて人工のネットワークをシミュレーションしてみます (triangle の係数をノード数で割っているのは、ひとまずおまじないと思って下さい)。

# Number of nodes
N <- 100
# Draw edges randomly
seed_network <- network::network(N, density = 0.1, directed = FALSE)
# Set coefficients
coef_edges <- -3
coef_triangle <- 1/N
# Simulate a network
sim_network <- simulate(
  seed_network ~ edges + triangle, 
  coef = c(coef_edges, coef_triangle),
  seed = 334
)
# Plot the simulated network
plot(sim_network)

f:id:komatsuna4747:20210907092533p:plain

それっぽいネットワークができあがりました。

ところが ERGM に基づいたネットワークのシミュレーションにも、問題点があります。少し天下り的ですが、以下の ERGM の尤度関数を考えます。

$\begin{align} \pi(g, \theta) = \exp\left(2 \alpha \sum_{i=1}^{n} \sum_{j=1}^{n} g_{ij} + \frac{6 \beta}{n} \sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{k=1}^{n} g_{ij} g_{jk} g_{ki}- \sum_{\omega \in \mathcal{G}} \exp(Q(\omega, \theta))\right) \end{align}$

ポテンシャル関数のパラメーターを $\alpha \rightarrow 2 \alpha$ , $2\beta/3 \rightarrow 6 \beta /n$ と置き換えたものです。ここから (i) $(\alpha, \beta) = (-1, 0.5)$ , (ii) $(\alpha, \beta) = (-1, 1)$ , (iii) $(\alpha, \beta) = (-1, 3)$ とパラメーターを設定し、異なる density のネットワークからシミュレーションを開始させ、その収束先を調べたものが以下の図です。図は生成されたネットワークの density をプロットしています。(使用したコードは長いので、末尾に付けます)。

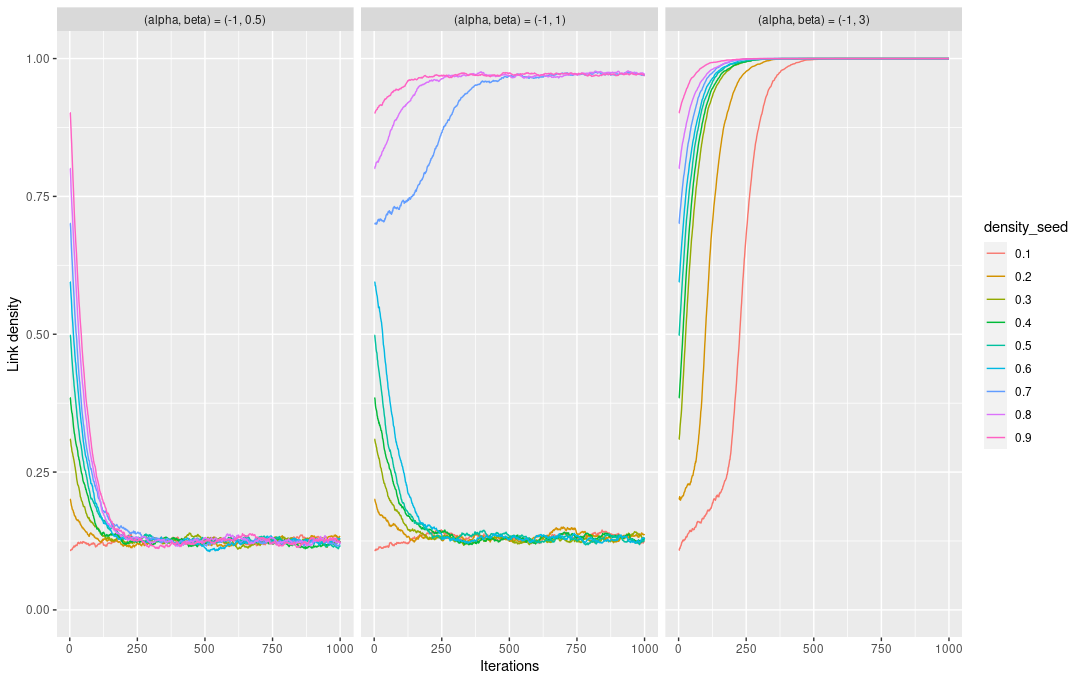
f:id:komatsuna4747:20210908020623p:plain

(i) のケース (上図左)では sparse なネットワークに、(ii) (上図中央) では最初のネットワークの density に応じて sparse/dense なグラフに、(iii) (上図右) のケースでは全てのノード同士がつながった完全グラフにそれぞれ収束していることがわかります。このように $\beta > 0$ (共通の友人の存在が当事者同士のつながりやすさに与える効果) が増加すると、収束先のネットワークが sparse なネットワークから dense なネットワークに変わり、中間のグラフが全てスキップされます。こうした現象は degeneracy と呼ばれたりします。

難点その2: ERGM から生成されるネットワークの構造は、パラメーターが変わると極端に変化する。

また ERGM で用いられる MCMCアルゴリズム、例えば Metropolis-Hasting は、ネットワークのリンクを1つずつアップデートしていきます。Mele (2017) はこれを local sampler と呼んでいます。Mele はネットワークの分布が双峰性 (bimodal) を示すとき、local maxima に一度たどり着くと、そこからlocal sampler で脱出するには指数時間かかることを示しています。これは図の (ii) のケースにあたります。理論上 (ii) のケースでは、sparse なネットワークの方に収束することがポテンシャル関数の global maxima に達することだとわかりますが、ネットワークの初期値によってはポテンシャル関数の local maxima にトラップされてしまいます。前回議論したゲームの複数均衡が、ここで問題となるわけです。

Identification

経済の人は、パラメーターの識別 (identification) を常に気にします。パラメーターの識別で確認することは、「観察可能な変数の分布から、興味のあるパラメーターが一意に定まるか」どうかです。識別はあるパラメーターの推定量が consistent であるための必要条件であり、推定量が信頼に値するかどうかを最低限保証するものです。

今考えるモデルで関心のあるパラメーターは、直接つながりの影響 ( $\alpha$ ) と、共通の友人の影響 ( $\beta$ ) です。特に $\beta$ は ERGM だからこそ考慮できるパラメーターであり、それが識別できるかどうかは重要です。

識別の議論は、サンプルサイズが無限であるような理想状態で行われます。ネットワークにおける理想状態とは、(i) 無限個のネットワークを観察できる, (ii) ある1つのネットワークのノード数が無限になる、の2通りがあります。(i) のケースの識別は容易 (と各所の論文に書かれているが、どれほど容易かは不明) であること、および一般に社会ネットワークを複数観察することは難しいことから、ここでは (ii) のネットワークのサイズが無限であるケースを考えます。このとき、 $\beta$ は識別できるのでしょうか。

答えは $\beta \geq 0$ のとき「No」、 $\beta$ が負のとき「Yes」です。しかしこれはあまり嬉しくありません。共通の友人がいる場合、つながりやすさに正の効果があると考えるのが自然ですが、その場合は観察された1つのネットワークからだけでは共通の友人の影響を識別できないからです。

難点その3: 外部性のパラメーターが全て非負であるとき、それらを識別することはできない。

実は今考えているモデルは、ある確率 $\mu^{*}$ による Erdos-Renyi model、つまり各ペアのリンクが確率 $\mu^{*}$ で独立に draw されるモデルと等価であることがわかっています (Chatterjee and Diaconis, 2013; Mele, 2017)。つまり、あるネットワーク $g$ を観察したとき、それが $\pi(g, \alpha, \beta)$ から出たものなのか、 $\pi(g, \alpha', 0)$ (ただし、 $\alpha'$ と $\mu^{*}$ の間にはある1対1の関係式が成立) から出たものかが、区別できないということです。

困りました。せっかく外部性を取り入れたモデルを考えたのに、場合によってはパラメーターを識別できないケースがでてしまいました。そうした問題がどうして発生してしまうのか、解決策はあるのか、機会を改めて見てみましょう。

Conclusion

本稿では、まずは R で ERGM を扱うことに慣れることから始め、ERGM に関わる問題点をあげていきました。本稿であげた問題点は以下の通りでした。

難点その1: リンク間の相互依存関係を考慮する時、ERGM の尤度関数の分母が現実的な時間内に計算不可能である。

難点その2: ERGM から生成されるネットワークの構造は、パラメーターが変わると極端に変化する。

難点その3: 外部性のパラメーターが全て非負であるとき、それらを識別することはできない。

それぞれ、理論的な観点、計算的な観点からいずれも challenging な課題です。次回以降、ERGM の概要を含めて掘り下げていきます。

References

Chatterjee, S., & Diaconis, P. (2013). Estimating and understanding exponential random graph models. Annals of Statistics, 41(5), 2428-2461.
Mele, A. (2017). A structural model of dense network formation. Econometrica, 85(3), 825-850.
Snijders, T. A. (2002). Markov chain Monte Carlo estimation of exponential random graph models. Journal of Social Structure, 3(2), 1-40.
鈴木努. (2018). 統計的ネットワーク分析の視座: 社会ネットワーク分析における意義の検討. 理論と方法, 33(1), 49-62.

シミュレーション用のコード

library(ergm)
library(magrittr)
library(foreach)
library(ggplot2)
library(doParallel)

# Number of nodes
N <- 100
# Set coefficients
coef_edges <- -1
coef_triangle <- c(0.5, 1, 3)
# Density of seed networks
density <- seq(0.1, 0.9, by = 0.1)
# Generate Erdos-Renyi networks for different densities
list_seed_network <-
  withr::with_seed(
    seed = 334,
    as.list(density) %>%
      purrr::map(function(x) network::network(N, density = x, directed = FALSE))
  )
# Compute densities of seed networks
density_seed_network <- 
  unlist(purrr::map(list_seed_network, network::network.density))
# Simulate networks for each combination of coefficients
cluster <- makeCluster(getOption("mc.cores", detectCores()-2), type = "FORK")
registerDoParallel(cluster)
df <-
  foreach(k = 1:length(coef_triangle), .combine = "rbind") %do% {
    coef_pair <- glue::glue("(alpha, beta) = ({coef_edges}, {coef_triangle[[k]]})")
    df_density <-
      foreach(i = 1:length(list_seed_network), .combine = "rbind") %dopar% {
        # Simulate networks
        density_sim_network <- 
          simulate(
            list_seed_network[[i]] ~ edges + triangle, 
            coef = c(2 * coef_edges, 6 * coef_triangle[[k]] /N),
            control = control.simulate.formula.ergm(MCMC.burnin = 0, MCMC.interval = 100, MCMC.prop.weights = "random"),
            output = function(x, iter, chain, ...) network::network.density(network::as.network(x)),
            nsim = 999,
            seed = 100 * 334 + 10 * k + i
          )
        output <- 
          tibble::tibble(
            coef = coef_pair, 
            density_seed = as.character(density[[i]]),
            iter = 1:(1+length(density_sim_network)),
            density = c(density_seed_network[[i]], unlist(density_sim_network))
          )
        return(output)
      }
    return(df_density)
  }
stopCluster(cluster)

g <-
  ggplot(data = df, aes(x = iter, y = density, group = density_seed, color = density_seed)) +
  geom_line() +
  ylim(0, 1) +
  xlab("Iterations") +
  ylab("Link density") +
  facet_grid(~ coef)
plot(g)