Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信

【ネットワークの統計解析】第7回　グラフラプラシアン・グラフフーリエ変換を簡単に振り返る

R&D データ分析 連載 機械学習

f:id:kur0cky:20201023211747j:plain

こんにちは． Sansan DSOC 研究開発部の黒木裕鷹です．また自粛期間が長くなってきましたね． 私も健康を取り戻さねばと思い，マルチビタミンやDHA，食物繊維を積極的に取り入れています．ハイボールに食物繊維を溶かすのが，罪悪感とアルコールが薄まり気分良く飲めるのでおすすめです．その名もトクホハイボールです．

さて，この連載では，自分の勉強・復習も兼ねて，ネットワークデータにまつわる（統計）解析を気の向くままに紹介しています． 前回の記事では，GNN を使った分析例として，拡散ネットワークからフェイクニュースを特定する論文を紹介しました． 今回の記事では，少し基本に立ち返り，GNN の基礎にもなっているグラフラプラシアン，そしてグラフフーリエ変換を復習したいと思います． 毎回のテーマに一貫性がないような気もしますが，ご容赦ください笑

グラフラプラシアン

この記事では，簡単化のため無向グラフのみを扱い，エッジの重複やループは許さないことにします．

グラフラプラシアン (graph laplacian) とは，グラフデータを表現する一つの形式です． グラフを表現する形式として最も有名なのは，隣接行列でしょう． グラフのノード数を Nとすれば，隣接行列 \bf Aは N\times Nであり，あるノード i, j間にエッジが張られていれば行列の (i,j),~(j,i)成分は1に，張られていなければ0となります． グラフラプラシアン \bf Lは，次式のように定義されます． ここで，行列 \bf Dは，対角成分に対応するノードの次数を持つような N\times Nの対角行列です．

 \displaystyle
{\bf L} := {\bf D} - {\bf A}.

また，正規化された行列を考え，次式のように定義されることもあります． ここで， \bf Iは単位行列で，正規化されたグラフラプラシアンでは対角成分がすべて1になっています．

 \displaystyle
\begin{align}
\tilde {\bf L} 
:=& {\bf D} ^ {-1/2}({\bf D} - {\bf A}){\bf D} ^ {-1/2} \\\
=& {\bf I} - {\bf D} ^ {-1/2} {\bf A} {\bf D} ^ {-1/2}.
\end{align}

さて，ここでひとつ例を考えてみましょう． たとえば次図のようなグラフを考えたとき，このグラフに対応する {\bf L}はどのようになるでしょうか．

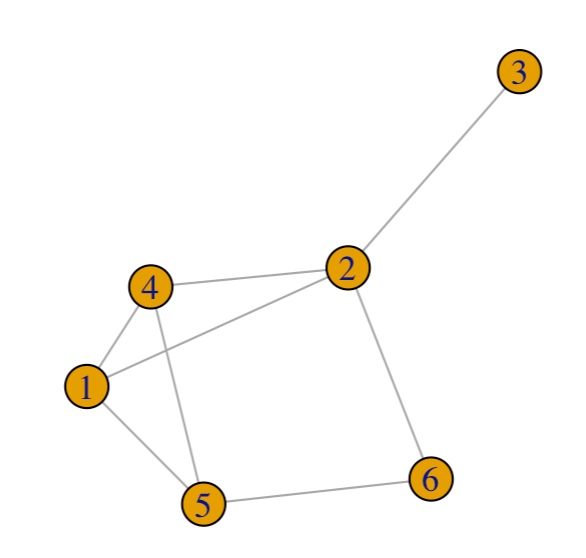
f:id:kur0cky:20210516190200p:plain
例

このグラフのラプラシアンは次式のようになります． たとえばノード1はノード2, 4, 5と接続しているため， {\bf L} _ {1, 2} = {\bf L} _ {1, 4} = {\bf L} _ {1, 5} = -1 に，そして次数は3となり {\bf L} _ {1, 1} = 3となります．

 \displaystyle
\begin{align}
  {\bf L} = \left(
    \begin{array}{cccccc}
    3 &  -1 &   0 &  -1 &  -1 &   0 \\\
   -1 &   4 &  -1 &  -1 &   0 &  -1 \\\
    0 &  -1 &   1 &   0 &   0 &   0 \\\
   -1 &  -1 &   0 &   3 &  -1 &   0 \\\
   -1 &   0 &   0 &  -1 &   3 &  -1 \\\
    0 &  -1 &   0 &   0 &  -1 &   2 \\\
    \end{array}
  \right)
\end{align}.

グラフラプラシアンの性質

ここからは，グラフラプラシアンがもつ性質について考えていきます． まず準備として，それぞれのノードに紐付く何らかの値（特徴量）を考え，このベクトルを \bf fとします．このような特徴量はグラフシグナル (graph signal) とよばれることがあります．

この節では，シグナル \bf fに対する次の2つの操作について，その性質を考えてみることにします．

  • 一次変換 {\bf L}{\bf f}
  • 二次形式 {\bf f} ' {\bf L} {\bf f}

まずは一次変換から考えてみます． グラフラプラシアンの定義より，一次変換は次式のように {\bf D}, {\bf A}の差を用いて分解することができます．

 \displaystyle
\begin{align}
{\bf h} & = {\bf L}{\bf f} \\\
& = ({\bf D} - {\bf A}) {\bf f} \\\
& = {\bf D}{\bf f} - {\bf A}{\bf f}.
\end{align}

さらに分かりやすくするため，グラフラプラシアンによって写像された新たなベクトル {\bf h}の各成分について考えてみます． ここで， d(v)はノード vの次数で， \mathcal N(v)はノード vの隣接ノード集合を表すとします．

 \displaystyle
\begin{align}
{\bf h} _ i 
& = d(v _ i) \cdot {\bf f} _ i - \sum _ {j = 1} ^ {N} {\bf A} _ {i, j} \cdot {\bf f} _ j \\\
& = d(v _ i) \cdot {\bf f} _ i - \sum _ {v _ j \in \mathcal N (v _ i)} {\bf A} _ {i, j} \cdot {\bf f} _ j \\\
& = \sum _ {v _ j \in \mathcal N(v _ i)} ({\bf f} _ i - {\bf f} _ j).
\end{align}

つまり，グラフラプラシアンによる写像は，近傍ノードのシグナルとの差を足し合わせたものになるということが分かりました．

同様に，グラフラプラシアンによる二次形式も考えてみましょう．

 \displaystyle
\begin{align}
{\bf f} ' {\bf L} {\bf f}
& = {\bf f}'{\bf h}\\\
& = \sum _ {v _ i \in \mathcal V} {\bf f} _ i \sum _ {v _ j \in \mathcal N (v _ i)} ({\bf f} _ i - {\bf f} _ j) \\\
& = \sum _ {v _ i \in \mathcal V} \sum _ {v _ j \in \mathcal N (v _ i)} ({\bf f} _ i {\bf f} _ i - {\bf f} _ i {\bf f} _ j) \\\
& = \sum _ {v _ i \in \mathcal V} \sum _ {v _ j \in \mathcal N (v _ i)} (\frac{1}{2} {\bf f} _ i {\bf f} _ i - {\bf f} _ i {\bf f} _ j + \frac{1}{2} {\bf f} _ j {\bf f} _ j) \\\
& = \frac{1}{2} \sum _ {v _ i \in \mathcal V} \sum _ {v _ j \in \mathcal N (v _ i)} ({\bf f} _ i - {\bf f} _ j) ^ 2.
\end{align}

上式より，グラフラプラシアンによる二次形式は，近傍ノードのシグナルとの差の二乗和をさらに足し合わせたものであり，シグナルが隣接するノードと異なる程度を表していると解釈できます． つまり，似たシグナルを持つノード同士が繋がる傾向にあるような，ホモフィリーのあるネットワークでは二次形式が小さくなる，ということです． 反対に，近傍ノードとの違いが大きいネットワークでは二次形式も大きくなる，ということです．

グラフラプラシアンの固有値ベクトル

続いてこの節では，グラフラプラシアンの固有値 \lambda，固有ベクトル {\bf u}について考えてみます．

 \displaystyle \lambda {\bf u} = {\bf L} {\bf u}.

まず，無向グラフのグラフラプラシアンは実対称行列であるため，実数の固有値をもちます． また，前節で考えたように二次形式が非負であることより，グラフラプラシアンは半正定値行列であり，固有値は非負となることもわかります．

さて，固有値が非負であることが分かったので，ここからは一般性を失うことなく小さい順に 0 = \lambda _ 0 \leq \lambda _ 1 \leq \dots \leq \lambda _ {N - 1} とし，対応する固有ベクトルを\displaystyle {\bf u} _ 0, {\bf u} _ 1, \dots, {\bf u} _ {N-1}と表します．ただし，固有ベクトルは長さが1になるように調整されているとします．

 \displaystyle
\lambda = \lambda{\bf u}^T{\bf u} = {\bf u} ^ T \lambda {\bf u} = {\bf u} ^ T {\bf L}{\bf u} \geq 0.

さらに面白い性質をひとつ紹介します． グラフ \mathcal Gが非連結であるとき，ラプラシアンの成分は連結部分ごとにブロック対角化できるため，固有値0の重複数は \mathcal Gの連結成分数に等しくなります．

先ほど例示したグラフの固有値，固有ベクトルを次式に示します．連結グラフでしたが，たしかに固有値0がひとつだけありますね． また，対応する固有ベクトルは全ての成分が同じになっていることも分かります．

 \displaystyle
\begin{align}
&  {\bf L} = \left(
    \begin{array}{cccccc}
    3 &  -1 &   0 &  -1 &  -1 &   0 \\\
   -1 &   4 &  -1 &  -1 &   0 &  -1 \\\
    0 &  -1 &   1 &   0 &   0 &   0 \\\
   -1 &  -1 &   0 &   3 &  -1 &   0 \\\
   -1 &   0 &   0 &  -1 &   3 &  -1 \\\
    0 &  -1 &   0 &   0 &  -1 &   2 \\\
    \end{array}
  \right), \\\
&  {\bf \lambda} = (0.0, 0.9, 2.0, 3.6, 4.0, 5.5), \\\
&  {\bf U} = ({\bf u} _ 0, {\bf u} _ 1, \dots, {\bf u} _ {5}) 
  =  \left(
    \begin{array}{cccccc}
 -0.41&  0.21& -0.41 & 0.15 & 0.71 &-0.32\\\
 -0.41& -0.08&  0.00 & 0.54 & 0.00 & 0.73\\\
 -0.41& -0.87 & 0.00& -0.21 & 0.00 &-0.16\\\
 -0.41&  0.21& -0.41 & 0.15& -0.71& -0.32\\\
 -0.41 & 0.31&  0.00& -0.77 & 0.00 & 0.38\\\
 -0.41&  0.21 & 0.82&  0.15 & 0.00 &-0.32
    \end{array}
  \right).
\end{align}

実は，固有ベクトル（大きさ N）を各ノードに対応させると，小さい固有値の固有ベクトルは穏やかに振動し，大きい固有値の固有ベクトルは激しく振動していることがわかります． Shuman et al. (2013) の Fig.2 を例として引用し，次図に示します． {\bf u} _ 0はすべて同じ値をとっていること， {\bf u} _ 1 では値がゆるやかに変化していること， {\bf u} _ 50では隣接するノード同士の値が激しく変化していることがそれぞれ分かります．

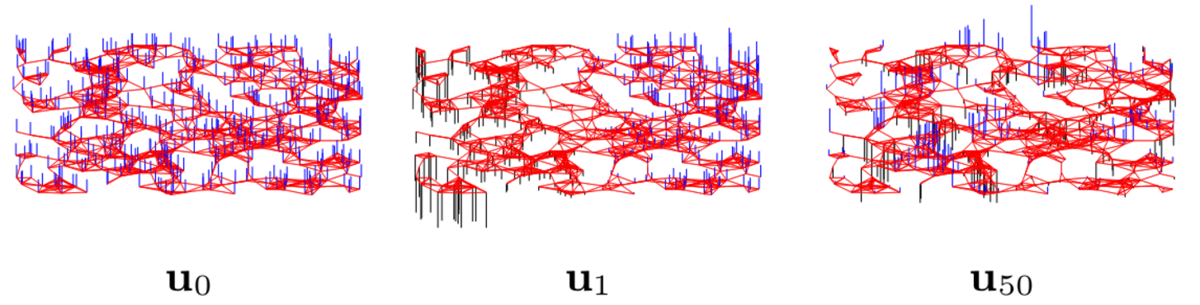
f:id:kur0cky:20210520002713p:plain
グラフラプラシアンの固有ベクトル (Shuman et al., 2013)

この図から，固有値 \lambda は周波数に，固有ベクトルは基底関数にそれぞれ対応していそうなことが分かりますね！！

グラフフーリエ変換

ここからは，いよいよグラフフーリエ変換について考えていきます． まず，通常の時系列のフーリエ変換は次式で与えられることを思い出します． ここで， f(t)は時間領域のシグナルで， \xi は任意の実数です．

 \displaystyle
\hat f(\xi) := \langle f(t), \exp(-2\pi it \xi) \rangle = \int _ {-\infty} ^ {\infty} f(t) \exp (-2\pi it \xi) dt.

時系列のフーリエ変換は，固有関数 \exp(-2\pi it\xi)とシグナル f(t)の積の積分で与えられることが分かります． つまり，これをフーリエ変換をグラフに対応させるならば，固有ベクトルとグラフシグナルの積の和を考えることになります． 実際に，グラフフーリエ変換は次式で与えらます．

 \displaystyle
\hat {\bf f} _ i := \langle {\bf f}, {\bf U} _ l \rangle = \sum _ {i = 1} ^ N {\bf f} _ i {\bf U} _ {i, l}.

また，まとめて行列で表すと次のようになります． グラフラプラシアンの固有ベクトルからなる行列を転置させ，グラフシグナルと内積を取ることで簡単に求められるということです．

 \displaystyle
\hat {\bf f} = {\bf U}' {\bf f}.

この操作により，グラフのノード領域にあったシグナルを，周波数領域のスペクトルに写すことができました． 逆に，スペクトルデータを周波数領域からノード領域に戻すならば，次式で与えられる逆フーリエ変換を行えばよいです．

 \displaystyle
{\bf f} = {\bf U} \hat {\bf f}.

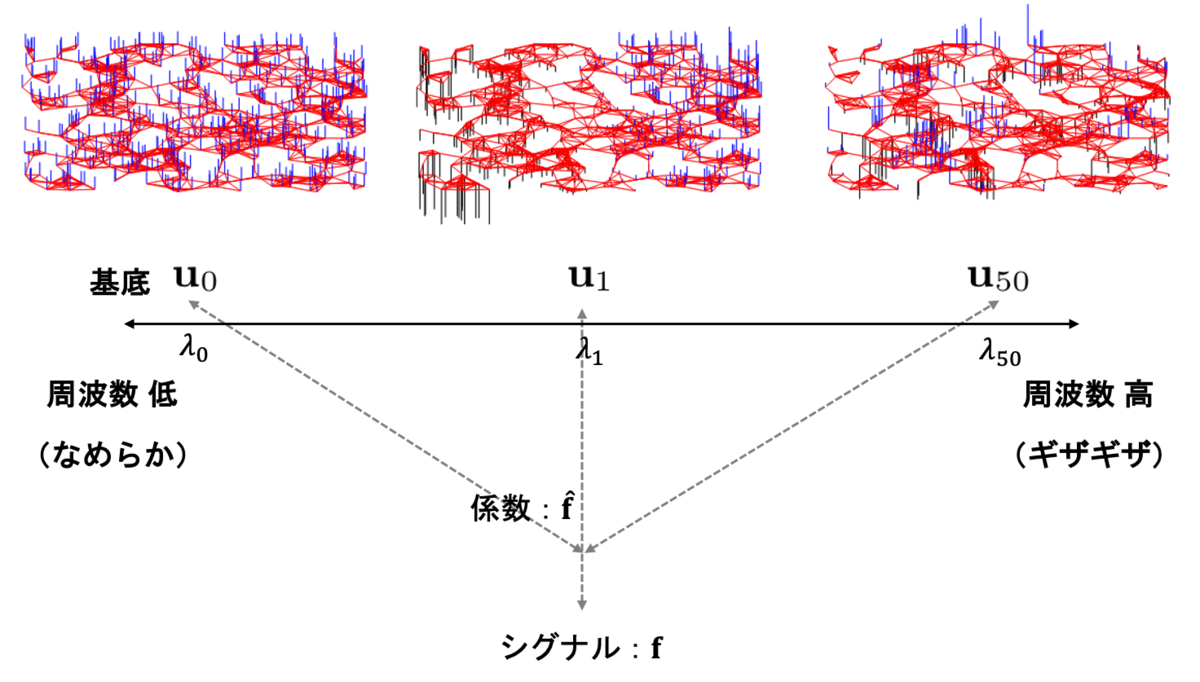
グラフフーリエ変換のイメージを整理しておきましょう． 周波数に対応する固有値 \lambda は，基底 {\bf u}の激しく振動する程度を表しています． また，これらの基底がどの程度シグナル \bf fに寄与しているかを示すのが，フーリエ変換により求まる係数 \hat {\bf f}です．

f:id:kur0cky:20210525032238p:plain
グラフフーリエ変換のイメージ

グラフ信号のフィルタリング

グラフフーリエ変換によってグラフシグナルをスペクトル領域に写すことができたため，通常の信号処理と同様にフィルタリングなどを行うことができます． 注目する周波数の寄与するシグナルのみを取り出し，逆変換でノード領域に戻す操作を行います．

f:id:kur0cky:20210520123400p:plain
フィルタリングのイメージ

念のため，次式のように数式でもフィルタリングを表しておきます． ここで， {\bf H}は N\times Nの対角行列で，対角成分には対応する周波数 \lambdaのフィルタ H(\lambda)をもちます．

 \displaystyle
{\bf f} _ {filtered} = {\bf U}{\bf H}{\bf U}'{\bf f}

たとえばノイズを取り除く目的でローパスフィルタを行う場合，高周波数の H(\lambda)を全て0にするなどの操作が考えられます．

おわりに

今回の記事では，スペクトラル GCN に欠かせないグラフラプラシアン・グラフフーリエ変換について簡単におさらいしました． GCNとの繋がりについては第5回記事で触れているので，ご覧頂ければ幸いです

buildersbox.corp-sansan.com

季節の変わり目で体調管理が厳しいですが，どうぞご自愛くださいませ．それでは

参考文献

  • Shuman, D. I., Narang, S. K., Frossard, P., Ortega, A., & Vandergheynst, P. (2013). The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE signal processing magazine, 30(3), 83-98.
  • 田中雄一. (2014). グラフ信号処理のすゝめ. 電子情報通信学会 基礎・境界ソサイエティ Fundamentals Review, 8(1), 15-29.


buildersbox.corp-sansan.com

© Sansan, Inc.