
こんにちは、Sansanの糟谷勇児です。
今回も実務に必要な統計学をガチャで考える話をやっていこうと思います。
第1回から読みたい方はこちら。
buildersbox.corp-sansan.com
いきなりですが皆さんは「にゃんこ大戦争」をやったことがありますか?
にゃんこ大戦争のガチャは普段は超激レアが当たる確率が5%なのですが、超極ネコ祭りの時には超激レアが当たる確率が10%まで増えるのです。2倍ですね。
ちなみに5%で当たりとしたときの50連ガチャ分布(N=50の二項分布)、つまり50連した時の当たり数とその確率の関係を書くとこんな感じになります。
いつもの高精度計算サイト様から作成しました。
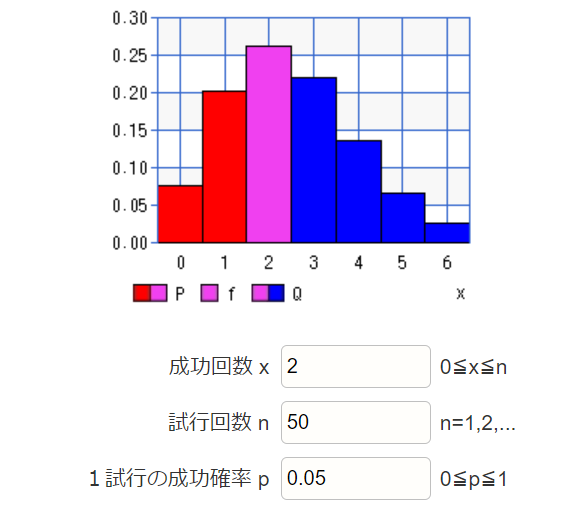
5%の超激レア率なら、50回回せば2個ぐらい当たるのが普通で、4個も十分(13%ぐらい)あり得る感じですね。
それが10%になるとこんな感じです。

7個当たっちゃってもおかしくないですね。夢が広がりんぐです。
そんなわけで、今日は5%の成功率が10%になるという話をもとに考えていくことにしましょう。
前回の第三回では統計的検定について説明しました。
- 示したいことと反対の仮説である帰無仮説を立てて
- それを前提として考えると実験結果が珍しすぎることを示し
- 結果的に示したいことを示す
ということでした。
今回はこれを実務に応用して、業務の施策の効果を検証することを考えてみましょう。
いつものように例から考えていきましょう。
あなたはテレアポで営業をしています。普段は100件電話をすると5件ぐらいアポが取れるので5%の成功率です。
毎日だいたい10件電話するので1週間で平均50件電話するとします。さて、先週あなたはテレアポの天才と言われる先輩のテクニックを勉強させてもらいました。そして今週1週間のテレアポではそのテクニックを使ってみました。使ってみたところなんと、50件中5件アポが取れたのです。つまり10%なので普段5%の2倍です。やっぱり先輩は天才だ!
と思ったところで我に返ると、普段から週に2,3件は取れているので+2件取れたわけですが、よく考えると2件ぐらいならたまたまな気もしてきます。さてこれはたまたまなのか??
前回紹介した統計的検定で考えてみましょう。
さて、統計的検定では、最初に示したいことを決めます。今回は先輩のテクニックでアポを取れる確率が上がったというのが示したいことです。次にそれに対して、帰無仮説を決めます。今回はアポが取れる確率はいつもと変わっていない(つまり5%のまま)ということにします。帰無仮説を仮定したときに、今回の結果を当てはめてみて、確率を求め(確率の値をp値と呼ぶ)、それが十分に低いか(珍しいか)を考えます。
帰無仮説を仮定したときに50件で5件のアポが取れるという今回の結果は珍しいのでしょうか。50連ガチャ分布(N=50の二項分布)で5件以上のアポが取れる(つまり50連ガチャで超激レアが5個以上当たる)確率を見てみると...
ちなみにいつも使わせてもらっている高精度計算サイト様だと、一定個以上当たる確率を見たい場合こうすると簡単に見ることができます。

大体p値が10%ぐらいですから、まあ珍しいかもしれませんが、たまたまかもしれない微妙なラインです。
さて、50件ではまだ微妙でしたが次の週も同じ傾向で合わせて100件だったらどうでしょうか。
p値が2.8%なのでたまたまである可能性はだいぶ低くなってきました。

ここまでくるともうたまたまじゃないと思ってもいいかもしれないですね。
ちょっと注意点
さて最初に50件テレアポして5件取れる可能性は帰無仮説においても10%程度あると話しましたが、それは残りの約90%の確率で元の仮説が正しいということを意味しているわけではありません。90%のほうは帰無仮説においてアポが獲得できる件数が4件以内に収まる確率でしかなく、それは仮説の信ぴょう性とはあまり関係ないのです。
ガチャで考えてみましょう。10%の確率で超激レアが当たるガチャがあります。皆さんはこんなことはありませんか?「今なら10%より高い確率で超激レアが当たる」という神の声が聞こえる気がするのです。そうして実際1回ガチャを引いてみたら当たったとします。でもそれは10%の確率でたまたま起こっただけかもしれません。そしてその時、90%の確率で神の声が正しかったということにはなりませんよね。
(え、ガチャの例えが逆にわかりにくいですかね)
さて、もう少し現実は
今回先輩のテクニックで2倍のアポ率になったわけですが、確かに2倍になれば割とp値が小さな値になってくれるのですが、現実にはそんなテクニックがあったらみんな使っていることでしょう。そうすると実際は1.5倍でもかなり効果的な施策といえるわけです。
では5%が7%になっているとすると何回ぐらい実験するとp値が0.05を下回るでしょうか。
このように「有用な結果を得るために何件ぐらいの実験(サンプル)が必要かというのを事前に見積もること」をサンプルサイズ計算と呼んだりします。
これについては次回詳しく考えていこうと思います。
さて、200回の実験ではどうでしょうか。200回の5%は10回、7%は14回です。5%の確率で成功することを帰無仮説としたときの14回以上となる確率はどうでしょうか。13%ぐらいなのでまだ、たまたまがありそうです。

では400回ではどうでしょうか。4.8%なのでやっとp値0.05より低くなりました。
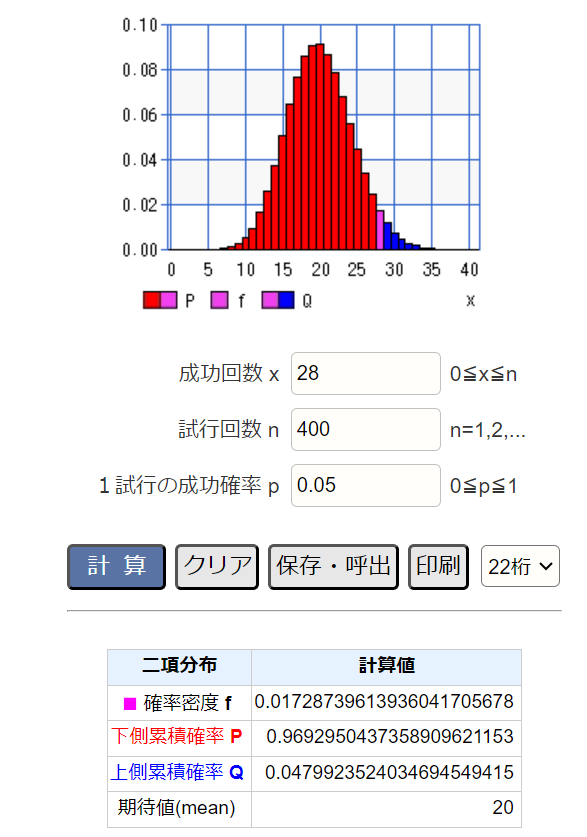
こう考えていくと実務でp値が十分低い値になることはなかなか難しいことがわかります。
なので「p値なんてどうでもいいじゃないか」というのは極論ですが、現実としてはp値が0.05を下回らなければ何もわかっていないと考えるのもまた極論です。
「まだサンプルは少ないのでたまたまかもしれませんが」というような枕詞を付けて先輩のテクニックをシェアしていくのは有用でしょう。並行してデータを増やして信ぴょう性を上げていってだんだん自信満々にシェアするようにすればいいのです。もちろん「もうちょっと集めてみたら、たまたまだった」ということもよくあるのでその時は正直に言いましょう。
また、定量の結果だけで考えず定性的にどんな効果があったのかを合わせて分析してシェアしていくことも大事です。
よりデータを集めていくなら一人でやるのではなく、うまく上司を説得してチームで行うことも必要です。
「この傾向が400回続けば統計的にも信ぴょう性が出てくる」と上司に説明し、検証回数の目標値を設定して、複数人で実験していくと早期に効果を確かめることができます。
「4人で2週間やってみます」など、何回検証するのか、それに何日かかるのか目標値が示されると上司も安心してGoを出すことができます。
とはいえなかなか考え方が難しいのも事実
ここまで、テレアポ業務がガチャのように一定の確率で成功したり失敗したりするというイメージで話してきましたが、実際はそう単純なものでもありません。景気の変動や予算の時期などによってアポが取れたり取れなかったりすることもありますし、どんなにテクニックがあっても買う気のないお客さんは会ってくれることはないでしょう。
そのような複雑な状況を考慮に入れるとしたら、どのように考えるべきかは統計学の経験値も必要になってきます。
あまり一人で考え込まず、周囲に詳しい人がいるなら、その人に相談して検証方法を考えていくのもよいと思います。
第3回でも話しましたが、数学的にはここからはたまたまだけど、ここからはたまたまではないというラインが明確にあるわけではありません。あくまでも自分たちの納得感としてどうなのかということでしかないのです。
4人で2週間やって結果が出たら次は自信をもって会社全体に広げていく、社外セミナーでも紹介していくなどです。
統計学的に考えるとは、このようなあいまいな状況を受け入れ、それでもベターな選択をできるように信じて進むということなのかもしれませんね。
それでは今回はこの辺りで。
次回はサンプルサイズについて考えていきましょう。