
こんにちは。研究開発部の糟谷勇児です。
今回は第二回ということで実務の場面を想定した話を書いてみようと思います。
前回はこちらです。
buildersbox.corp-sansan.com
前回は単発ガチャ(1連ガチャ)で出る当たりの数と確率の関係を表す1連ガチャ分布(ベルヌーイ分布)と10連などのN連ガチャで出る当たりの数と確率の関係を表すN連ガチャ分布(二項分布)を紹介しました。
ところで前回は「ドラクエウォーク」を例に話しましたが、私は「ヘブンバーンズレッド」というゲームもやっています。
こちらのガチャは最高レアであるSSが出る確率が3%となっています。
つまり1連ガチャ分布(ベルヌーイ分布)はこんな感じのグラフになります。

10連ガチャ分布(N=10の二項分布)はこういうグラフになります。
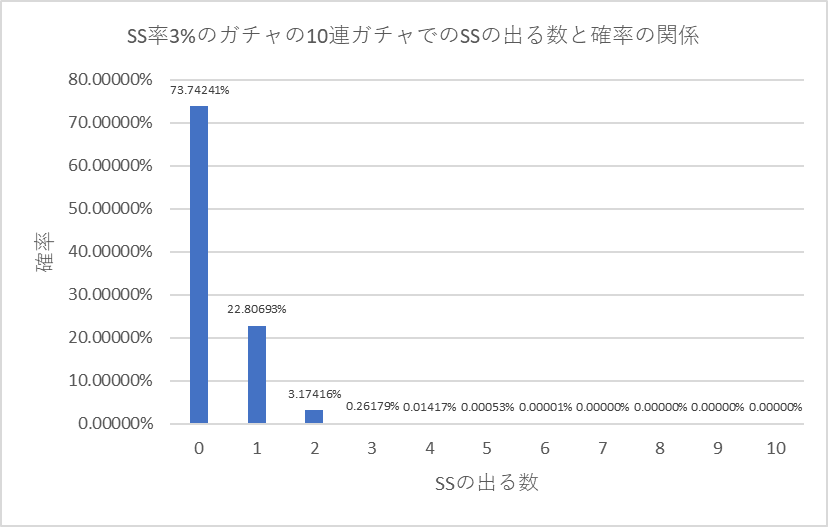
さて今回は文字認識などの認識精度について考えてみましょう。
精度というと難しく感じてしまいますが7連ガチャで簡単にイメージできるという話をしていこうとおもいます。
近年、機械学習が製品やサービスに使用されることが増えてきて、「この文字認識の精度はXXパーセントだ」、「このリコメンドエンジンのコンバージョン率は○○パーセントだ」などのようにパーセントを使うことが増えてきました。
今回はパーセントをガチャのイメージを使って正しくとらえることを目標にしましょう。
具体的に考えるために以下のような設定にしてみます。
あなたはあるサービスの商品企画をしていますが、そのサービスでは郵便はがきを住所ごとに仕分ける必要があります。
そこであなたは郵便番号7文字を認識する文字認識エンジンの開発を研究開発部に依頼しました。
そのエンジンのプロトタイプが研究開発部から納品されて、認識精度は一文字当たり97%だったとします。
なんかすごそう。センター試験効果
さて、97%というとなんかすごそうな気がしませんか。私だけですかね。
私の経験から、多くの人はパーセントの話が出てくると無意識に自分になじみ深いパーセントと比較することがあるようです。
それは例えば学校のテストなどです。センター試験で97%も取れば東大合格も夢じゃないですし、大学のテストなら「優」がつくでしょう。
そのようなイメージからなんとなく90%を超えるといい感じな気がして、80%を超えるとまあまあ及第点かななんて思ってしまう現象を私は勝手にセンター試験効果と呼んでいます。
(今やセンター試験じゃなくて共通テストらしいですが、おじさんにはなじみがないのでセンター試験と呼んでいます)
実際には認識精度のパーセンテージが十分か不十分かは利用用途ごとに考えなければならず、雰囲気でいい悪いを判断しても生産的な議論はできないでしょう。
そこでガチャで考えてみる
さて、1文字当たりの認識精度が97%ということは、ヘブンバーンズレッドのガチャでSSが出る率と認識ミス率が同じですから、同じように考えてみることができそうです。
7文字を正確に認識できる割合は、ガチャに例えると7連ガチャをしたときに1回もSSが出ない確率ということになります。
7連ガチャぐらいすれば結構、SSが出そうな気がしませんかね。
実際計算してみると、すべて97%のほうに入ればいいので
0.97×0.97×0.97×0.97×0.97×0.97×0.97=0.97の7乗=80.7%
となります。5枚のはがきがあれば平均一つぐらい間違う確率です。
ざっくり分けて後工程でミスが修正できるならこれでもいいかもしれませんが、
これ単体ですべての仕分けをするのは難しいかもしれませんね。
というわけで、精度などのパーセンテージを印象で考えず、利用用途に応じてN連ガチャ分布(二項分布)で具体的に考えてみようという話でした。
でも認識精度とガチャは同じように考えていいの?
しかし、ガチャは誰がいつ引いても同じ確率ですが、認識精度はどうでしょうか。
文字認識なら字がきれいな人とそうでない人、認識しやすい字と間違いやすい字などで認識できる確率は変わるでしょう。
とはいえ、今回のような例だと、字がきれいな人かどうか、何の数字が来るかはほぼランダムなので、
どんな文字が次に来るか、どんな人が書くか自体もガチャですので、全体的にガチャと同じように考えて良いとみなすことができます。
(厳密には汚い字を書く人は7文字のうち複数の文字をミスしてしまう可能性も高いので、実際のデータでも検証は必要になります)
一方で、フィードバックがある場合、つまり数字を書く人の目の前で認識結果を見せるような場合はだんだんと認識しやすい字を書いてくれるようになったりするので、だんだん良くなっていく影響がある場合があり、その場合はガチャとは状況は異なるかもしれません。
しかしざっくりガチャと同じだととらえて、そこからさらにいい影響も出るかもぐらいに分けて考えると進めやすいと思います。
まとめとか
そんなわけで、認識精度のパーセンテージについての話でした。
なお、手書きの数字の認識は書かれている場所さえわかれば実際は99.9%を超える精度で行うことがかなり昔からできています。
そのことはこちらのブログでも書きました。
歴史をたどってディープラーニングを学ぶ 第十六回 これまでのまとめと、なぜ私はディープラーニングをつくれなかったか - Sansan Tech Blog
とはいえいろいろな条件次第で、パーセンテージは変わってきますので、使う場面に応じて評価することで大失敗を防ぐことができます。
また、今回のように全ての文字の認識が成功して初めて効果を発揮するようなシーンではN連ガチャ分布(二項分布)で考えることが重要です。
別の例としては法人番号13桁を認識する場合が考えられます。この場合は13連ガチャ分布(N=13の2項分布)で検討するとよいでしょう。ただし、法人番号は最後の桁がチェックデジットと言って全部の数字を足して11で割った余りが入っているので、1文字以内のミスはミスと分かりますので、ミス0の場合とミス1の場合の足し算して
f(0)+f(1)
で見積もってもいいかもしれません。
なお、どうしても現実と計算で求めた確率には差が出てくるので、実際のデータで実験をすることは必須です。
また、5枚のうち1枚間違っているなら使い物にならないと最初からはねのけるのではなく、今の精度で活用するとしたらどうするか考えることも大事です。
例えば最初3桁だけでわかる都道府県の判定でソリューションとして成立するならば3連ガチャで考えることができます。
研究開発する側もどのようにしたら実際のソリューションで活用できるのか一緒に検討していくことが大事ですね。
そんなわけで、機械学習や認識のパーセントをガチャでリアルに考えてみようという話でした。
次回は統計的検定について書いていこうと思います。