名寄せの定量評価とGroup Sequential Test

こんにちは、技術本部Sansan Engineering UnitのNayoseグループでバックエンドエンジニアをしている上田です。

普段はデータの名寄せサービスを開発しています。Sansanの名寄せというのは、こちらのページに記載のとおり、別々のデータとして存在する同じ会社や人物のデータをひとまとめにグルーピングすることを言います。

下記の記事のとおり、前回は名寄せアルゴリズムを定量評価する際に利用する統計的仮説検定において、固定サンプルサイズ検定の課題を解決する逐次検定の手法SPRT（Sequential Probability Ratio Test、逐次確率比検定）を紹介しました。SPRTには別の課題があるため、今回は実務で重宝する特徴をもつGroup Sequential Testという逐次検定について紹介します。
buildersbox.corp-sansan.com

この記事の要約

Group sequential test（GST）を使えば、サンプルサイズを削減しつつ、事前に検定を終了する日付を決められる（シミュレーションでは約25%のサンプルサイズを削減）
GSTにアルファ消費を導入することで、任意のタイミングにおける棄却域を決められる
前半にアルファ消費を抑えるO'Brien-Fleming-like型やKim & DeMets Power family型、Hwang, Shih & DeCani Gamma family（ $\gamma < 0$ ）型のエラー消費関数を用いることで高い検出力を得やすくなる

名寄せの定量評価とSPRTの課題

業務では新しい名寄せアルゴリズムを開発することがあります。
アルゴリズム開発の基本戦略は、ユーザーが取り込んだ名刺と、マスターとして存在する会社データを同じ会社としてグルーピングできたら正解、別の会社のデータをひもづけてしまったら不正解と定義して、その正解率を高めるアルゴリズムを採用するというものです。

そして、その定量評価には統計的仮説検定を用いることがありますが、サンプルサイズを固定して行う一般的な仮説検定には実務利用に対して以下の課題があります。

サンプルサイズを事前に決めないといけない
そしてそれは非常に大きいサイズとなる
その大きなサンプルサイズに対して、全件を調査した後でなければ評価できない（検定の多重性の問題*1）

この課題を解決する1つの検定手法として、事前にサンプルサイズを決める必要なく、1件ずつ観測と検定をする逐次確率比検定（Sequential Probability Ratio Test; SPRT）を前回の記事で紹介しました。

ただ、この手法には以下の欠点があります。

検定終了までの平均試行回数は小さいですが、効果量が小さい場合*2などで検定が終わらない場合があります。これは、実務に存在する作業期限やデータ数に上限がある場合には使いづらくなります。
事前にサンプルサイズを見積もれないため、作業時間の見積もりが困難です。
バッチ処理的に評価できません。バッチ処理できないと、1件ずつのサンプリング（観測）と検定を繰り返す必要があり、手順が多くなるという意味で非効率的です。

今回はこの欠点を克服するGroup Sequential Test（GST）を扱います。

Group Sequential Test（GST）の概要

ここではKim and Tsiatis（2020）のレビュー記事を参考にGSTの概要を紹介します。

GSTはサンプルサイズを事前に決める代わりに、検定の最後のデータを収集する前に行う評価（中間解析、Interim analysis）の回数を事前に決めます。例えば、データ分析の締め切りが10日後であれば、1日1回の解析をすることとして合計10回の中間解析で検定をする計画にする、などです。

例えば、A/Bテストとして2つの群A、Bのそれぞれの母平均の差の検定（母分散は既知）を考えます。
それぞれの標本空間から得られる確率変数 $X_A,\, X_B$ は、それぞれ平均 $\mu_A,\, \mu_B$ 、分散 $\sigma^2$ の正規分布に従うとします。
このとき、帰無仮説 $H_0:\, \mu_A = \mu_B$ 、対立仮説 $H_1:\, \mu_A \ne \mu_B$ を有意水準5%で $n$ 件の固定サンプルサイズ検定をする場合、検定統計量 $Z$ について

$\displaystyle |Z| = \left| \frac{\bar{X}_A - \bar{X}_B}{\sqrt{2\sigma^2/n}} \right| > 1.96$

となるときに、 $H_0$ を棄却します。ここで、 $\bar{X}_A,\, \bar{X}_B$ はそれぞれA群, B群の標本平均です。

ここで、中間解析の回数を $K$ 回とし、各中間解析で一定の $n$ 件を各群からサンプリングするとします。
$N(\mu,\, \sigma^2)$ が平均 $\mu$ 、分散 $\sigma^2$ の正規分布を表すとき、 $j\, (j = 1,\, \dots,\, K)$ 番目の中間解析における統計量 $Y_j$ について

$\displaystyle Y_j = \frac{\bar{X}_{Aj} - \bar{X}_{Bj}}{\sqrt{2\sigma^2/n}} \sim N(\delta^{*},\, 1)$

となります。ここで、 $\delta^{*} = (\mu_A - \mu_B)/\sqrt{2\sigma^2/n}$ です。
そして、 $k$ 番目の中間解析の時点のスコア統計量

$\displaystyle S_k = \sum_{j=1}^{k} Y_j \sim N(\delta^{*}k,\, k)$

または統計量

$\displaystyle Z_k = \frac{S_k}{\sqrt{k}} \sim N(\delta^{*} \sqrt{k},\, 1)$

いずれかについて、以下が成り立つとき、 $k$ 番目の中間解析の時点で $H_0$ を棄却します。

$\displaystyle |S_k| > b_k,\, \text{または} |Z_k| > c_k$

ここで、検定全体の第一種の誤りの大きさを $\alpha$ としたとき、棄却域 $b_k,\, c_k$ は $H_0$ の下で以下を満たします。

$\displaystyle \begin{align} & \Pr( |S_{1}| < b_1, \dots, |S_{K}| < b_K) \\ =& \Pr( |Z_{1}| < c_1, \dots, |Z_{K}| < c_K) \\ =& 1 - \alpha \end{align}$

このように検定するのがGSTの基本です。
SPRTではその逐次検定における第一種、第二種の誤りの大きさを用いて近似的な棄却域が得られましたが、GSTの場合はどうするのでしょうか。

さまざまな棄却域とアルファ消費

GSTを初期に研究し、棄却域を与えたArmitage et al.（1969）, Pocock（1977）, O’Brien and Fleming（1979）は各中間解析でのサンプルサイズを一定として、これを計算していました。
ただ、実際の検定の段階でその制約とおりのサンプルサイズを得られる保証はありません。つまり、応用上この制約はない方が良く、任意の中間解析の時点で任意のサンプルサイズで中間解析できる方が応用に富んでいます。

Slud and Wei（1982）はこの問題に対し、 $k$ 番目の中間解析における有意水準 $\alpha_k$ を検定全体の有意水準 $\alpha$ に対して $\sum_k \alpha_k = \alpha$ になるような中間解析の有意水準を求めるアプローチを提案しました。
この考えをLan and DeMets（1983）が発展させ、 $\alpha_k$ を単に任意に設定するのではなく、中間解析ごとに全体の $\alpha$ を消費/支出する（ $\alpha$ -spending）という表現と概念を導入しました。
これは、第一種の誤りの確率をエラー消費関数 $\alpha^{*}(t)$ に合わせて各中間解析に配分するというものです。GSTは多重検定の一種になります。アルファ消費によって検定全体の有意水準 $\alpha$ を超えないように、逐次実行する各回の有意水準をコントロールできるようにした訳です。

エラー消費関数は、情報分数（または情報時間） $t$ , $0 \le t \le 1$ , の単調非減少関数で、 $\alpha^{*}(0)=0,\, \alpha^{*}(1)=\alpha$ を満たします。
そして、 $k=1, \dots, K$ 回目の中間解析の時点のアルファを $\alpha_k = \alpha^{*}(t_k) - \alpha^{*}(t_{k-1})$ として配分します。

以下に代表的なエラー消費関数を記載します（Georgi（2019） p.168参考）。

表1：代表的なエラー消費関数
エラー消費関数	名称
$\displaystyle \alpha^{*}(t) = \alpha \ln(1 + (e - 1)t)$	Pocock-like
$\displaystyle \alpha^{*}(t) = 2 \left( 1 - \Phi \left( \frac{z_{\alpha / 2}}{\sqrt{t}} \right) \right)$	O'Brien-Fleming-like
$\displaystyle \alpha^{*}(t) = \alpha t$	Uniform
$\displaystyle \alpha^{*}(t) = \alpha t^{\rho}, \, \rho > 0$	Kim & DeMets Power family
$\displaystyle \alpha^{*}(t) = \begin{cases} \displaystyle \alpha \cdot \frac{1 - e^{-\gamma t}}{1 - e^{-\gamma}} & \gamma \ne 0 \,\text{の場合} \\ \alpha t & \gamma = 0 \,\text{の場合} \end{cases}$	Hwang, Shih & DeCani Gamma family

また、有意水準5%の場合のそれぞれのエラー消費関数をグラフにしました。

図1：有意水準5%のときのPocock-like, O'Brien-Fleming-like, Uniformそれぞれのエラー消費関数

これを見ると、Pocock-likeは中間解析の前半から多めのアルファを消費し、逆にO'Brien-Fleming-likeは後半から多めに消費するような保守的な戦略を取っていることが分かります。

図2：有意水準5%のときのKim & DeMets Power familyエラー消費関数

Kim & DeMets Power familyの場合、O'Brien-Fleming-likeのような後半にアルファをより消費する形で、 $\rho$ を大きくすればするほど、前半が保守的になっています。

図3：有意水準5%のときのHwang, Shih & DeCani Gamma family（HSD）エラー消費関数

Hwang, Shih & DeCani Gamma familyの場合は、パラメータ $\gamma > 0$ のときにPocock-likeのように攻めており、逆に $\gamma < 0$ のときに保守的なアルファ消費となっています。

このエラー消費関数を実際に用いる場合は、各中間解析でサンプルサイズが一定の場合は、 $t_k = k/K$ となります。
事前に検定全体で観測する最大サンプルサイズ $N$ を決めている場合は、k回目の中間解析で $n_k$ 件のサンプルを得た場合、 $t_k = \sum_{j=1}^{k} n_j / N$ となります。

サンプリングサイズが一定ではない場合の再計画と情報分数について

アルファ消費を用いる場合、仮に中間解析で事前に想定していたサンプルサイズを得られなかった場合にでも、柔軟に検定を再計画できます。
具体的には以下の手順となります。

1. 検定の計画時に、1回あたり20件（ $n_k = 20$ ）のサンプリングを行い、合計5回（ $K = 5$ ）の中間解析をするとします。
2. このときの情報分数列は(0.2, 0.4, 0.6, 0.8, 1.0)となり、エラー消費関数をO’Brien and Fleming型にしたとします。そのとき、以下になります。
- 累積消費アルファ列は(0.000001078, 0.0007883, 0.007616, 0.02442, 0.0500)
- 棄却域列は(4.877, 3.357, 2.680, 2.290, 2.031)
3. 3回目で30件のサンプルを得た場合、この時点で得られる情報量が変わってくるため、再度エラー消費を計算し直します。
4. 仮に、残りの4, 5回目のサンプルサイズを予定の残数30件を等分して15件ずつになるようにする場合、情報分数列は(0.2, 0.4, 0.7, 0.85, 1.0)のように更新されます。
5. この結果で再度棄却域を計算すると以下になります。
- 累積消費アルファ列は(0.000001078, 0.0007883, 0.01477, 0.0301, 0.0500)
- 棄却域列は(4.877, 3.357, 2.445, 2.231, 2.051)

更新前後での累積消費アルファをグラフにしてみました。

エラー消費関数を用いると、このように中間解析の柔軟性が増します。
ただし、ここまでの理論の前提として、実は各中間解析の結果は独立であるという前提があります。
よって、中間解析間で独立にならない場合、例えば上記のような中間解析の途中の再計画を乱用した場合には、あらかじめ設定した検定全体の第一種の誤りが増大することが指摘されています。
例えば、小山（2001）は1回目の中間解析の結果に応じて中間解析の回数を1回追加する場合の、棄却域の調整方法を提案しています。

GSTにおけるサンプルサイズは以下の疑問がありますが、これらは情報分数を用いて理解を深められます。

各中間解析で平均何件のサンプルサイズが必要か
全体で最大何件のサンプルサイズを必要とするか

一般的に、情報分数は $k$ 回目の中間解析時点のフィッシャー情報量 $I_k$ と最終回となる $K$ 回目のそれとの比で表されます。

$\displaystyle t = \frac{I_k}{I_K}$

エラー消費関数を使う場合、情報分数の分母は以下で与えられます。

$\displaystyle I_{K} = \left( \frac{z_{\alpha/2} + z_{\beta}}{\gamma} \right)^{2} R_{\text{inflation}}$

ここで、 $\gamma$ は対立仮説における効果量、 $R_{\text{inflation}}$ は固定サンプルサイズ検定のフィッシャー情報量に対するインフレーション因子と言われます。
一方、分子の情報量は、その時点の効果量の推定値の分散から得られます。

$\displaystyle I_k = \frac{1}{\text{Var}(\hat{\gamma}_{k})}$

この表現を使うと、任意の時点、任意のサンプルサイズでの情報分数、つまり棄却域を計算することが可能になります。

GSTの平均中間解析回数と検出力のシミュレーション

GSTは事前に検定を終わらせる時間（回数）を設定できる実務利用で嬉しい特徴を持っていますが、通常の固定サンプルサイズ検定と同様にサンプルサイズをむやみに小さくした場合の検出力が心配になります。
そこで、逐次検定のメリットである早期に検定を終了させる効果と検出力の関係について、シミュレーションして確認してみます。

ここで想定する実験は、前回記事でもご紹介したように、1件のサンプルに対して名寄せの正解・不正解を判断する二値分類を考え、正解の割合（名寄せの精度）を考えることにします。
この場合、名寄せの精度は二項分布のパラメータについて仮説検定することになります。

今回はA/Bテストのように、2つのアルゴリズムの精度をGSTで検定することにします。
このとき、時点 $k$ における検定統計量は以下になります。

$\displaystyle Z_k = \frac{\hat{p}_{Ak}-\hat{p}_{Bk}}{\hat{\sigma}_{k}}$

ここで、

$\displaystyle \hat{\sigma}_k = \sqrt{\frac{\hat{p}_{Ak}(1-\hat{p}_{Ak})}{n_{Ak}}+\frac{\hat{p}_{Bk}(1-\hat{p}_{Bk})}{n_{Bk}}}$

で、 $\hat{p}_{Ak},\, \hat{p}_{Bk}$ はそれぞれA, B群の $k$ 時点における母比率の推定値、 $n_{Ak},\, n_{Bk}$ はそれぞれA, B群における $k$ 時点の累積サンプルサイズとします。

この検定統計量を用いて、 $\delta = p_A - p_B$ について帰無仮説: $\delta = 0$ とし、対立仮説として以下4つを設定し、それぞれを片側検定することにします。

1. $p_A$ の真の値0.96, $p_B$ の真の値0.95のとき、 $\delta > 0$
2. $p_A$ の真の値0.94, $p_B$ の真の値0.95のとき、 $\delta < 0$
3. $p_A$ の真の値0.99, $p_B$ の真の値0.95のとき、 $\delta > 0$
4. $p_A$ の真の値0.90, $p_B$ の真の値0.95のとき、 $\delta < 0$

シミュレーションの条件は以下とします。

$\alpha$ （第一種の誤り）: 0.05
$\beta$ （第二種の誤り）: 0.20
中間解析回数: 20回
最大サンプルサイズ：固定サンプルサイズに対して、10%, 50%, 100%, 150%
各中間解析のサンプルサイズ: 固定サンプルサイズを中間解析回数で等分した件数
エラー消費関数: Pocock-like, O'Brien-Fleming-like, Kim & DeMets Power family, Hwang, Shih & DeCani Gamma family
シミュレーション回数: 1,000回

こちらのRスクリプトを使ったシミュレーション結果を以下に示します。

表2: Kim & DeMets Power family（ $\rho = 3$ ）, 固定サンプルサイズの100%の場合
$p_A$ の真の値	0.96	0.94	0.99	0.90
中間解析の平均回数	14.841	14.926	15.186	14.681
固定サンプルサイズ	5313	6426	224	343
平均サンプルサイズ	3933	4791	167	250
サンプルサイズ削減率	26%	25%	25%	27%
帰無仮説を棄却した回数	786	774	795	796
検出力	0.786	0.774	0.795	0.796

図5: Kim & DeMets Power family（ $\rho = 3$ ）について、サンプルサイズごとの検出力

図5: Kim & DeMets Power family（ $\rho = 3$ ）について、サンプルサイズごとの検出力

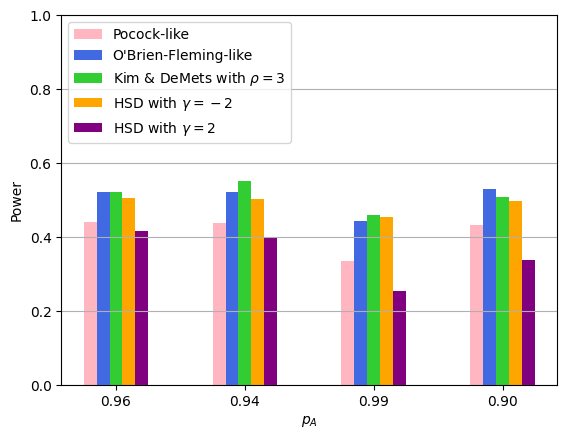
この結果から分かることは以下です。

固定サンプルサイズに対して約25%のサンプルサイズを削減できた
最大サンプルサイズを大きくすると検出力が向上した
エラー消費関数ごとの比較では、Pocock-likeのような前半により多くのアルファを消費する場合には検出力が小さくなった

実際の利用例

実際の業務では、名寄せ精度について本番リリース後のリグレッション確認の用途で利用しています。
例えば、中間解析を1日1回と決め、合計10日〜20日ほど中間解析を継続しています。
そのときの検定統計量と棄却域の様子をプロットした実際のグラフを以下に示します。

エラー消費関数の選択は試行錯誤中です。一旦はGeorgi（2019） p.170の以下の意見を参考にKim & DeMets Power familyのおいて $\rho = 3$ としたものを利用しています。

The choice of spending function can, in theory, be different for each A/B test. Due to considerations related to external validity (discussed in Chapter 12) the author’s recommendation is for using spending functions which are quite conservative early on. A Kim-DeMets power function with ρ = 3 seems to be a good compromise between ending tests as early as possible, and achieving a representative sample.

また、今回は紹介しなかったベータ消費（Beta-spending）を取り入れ、これ以上の中間解析を続けても意味がないことを結論付ける無益性境界（Futility bounries）を取り入れたGSTも一部導入しています。
その場合、その無益性境界を越えた場合に強制終了するbinding bounries型とその判断を任意とするnon-binding boundariesがあります。
ただ、ベータ消費関数の実務利用に関する知見はまだ収集中という状態のため、今後最適化できるようにしたいと考えています。

まとめ

Group sequential test（GST）を使えば、サンプルサイズを削減しつつ、事前に検定を終了する日付を決められる（シミュレーションでは約25%のサンプルサイズを削減）
GSTにアルファ消費を導入することで、任意のタイミングにおける棄却域を決められる
前半にアルファ消費を抑えるO'Brien-Fleming-like型やKim & DeMets Power family型、Hwang, Shih & DeCani Gamma family（ $\gamma < 0$ ）型のエラー消費関数を用いることで高い検出力を得やすくなる

あとがき

Webバックエンドエンジニアの私がGSTに出会い、本稿を投稿するに至った経緯を最後に紹介させてください。

私は大学で物理学を専攻し、量子論や熱統計力学などで確率・統計の基礎を学びました。その後、アクチュアリー（保険数理人）という職を目指したことがあり、改めて確率・統計を学びました。何とかアクチュアリーの数学試験に合格して日本アクチュアリー会研究会員（一番下のランク）になって以降、社会人エンジニアとしてキャリアをスタートさせていたため、その知識は眠ったままでした。

その後、Sansanで名寄せというドメインに向き合う中で、データ分析業務を行い、統計学を実務で使うようになりました。
業務で固定サンプルサイズの課題に直面しているさなかに、学生時代にアクチュアリー試験勉強用に買っていたP.G. ホーエル「入門数理統計学」の第13章に逐次解析という章があることを発見しました。試験勉強中の当時、この章は試験範囲外なので読んでもなければ関心もありませんでした。この章を十数年後に発掘して、前回の記事のようにSPRTの理論を実務で使うようになったのです。

ただ、いざSPRTを使ってみると、検定がいつ終わるのかわからないという課題にすぐに直面しました。そんな中、たまたまRSSで流れてきたSpotify R&Dの”Choosing a Sequential Testing Framework — Comparisons and Discussions”という記事が目に留まり、何のテストの話だろう？と読んで知ったのがGSTでした。

振り返ると、いまSansanの名寄せドメインの業務にGSTを導入しているのは、偶然的な出会いの上に成り立っているかもしれないということです。本当は課題ベースで向き合って解決策を探す方が良いのかもしれませんが、その際には知識の幅が必要になってきます。普段の活動の地続きで得られる知識には限界があり、別の角度や視点、時間軸で蓄積された知識というのが、時にブレイクスルーになることがあることを今回体験しました。

知識との偶然の出会いが業務課題を解決していると考えると、素敵だなと思います。
この記事が誰かの偶然の出会いにつながり、課題解決の一助になれると良いなと思って執筆しました。

最後まで読んでいただきありがとうございます。

*1:多重比較問題（Wikipedia）参照

*2:近似的にサンプルサイズの期待値がZ統計量の期待値の逆数（ $E[Z]^{-1}$ ）に比例するため。 A. Wald, Sequential Tests of Statistical Hypotheses, Ann. Math. Statist. 16(2): p.143, 1945, https://projecteuclid.org/journals/annals-of-mathematical-statistics/volume-16/issue-2/Sequential-Tests-of-Statistical-Hypotheses/10.1214/aoms/1177731118.full