歴史をたどってディープラーニングを学ぶ第七回　意外と難しいソフトマックス層を実装して学ぶ

こんにちは、ニューラルネット老人こと糟谷勇児です。
私はドラクエウォークという位置情報を使ったゲームをしています。
ウォークという名前ですが今回のウイルスの件で完全在宅ゲームになって歩く必要がなくなりました。

ドラクエといえば、ストーリーの序盤で圧倒的な力で主人公たちを打ち砕く強大な敵を、中盤で成長した主人公が打ち倒す展開が熱いですよね。
代表的な敵としてはムドーとかゲマとか。

ディープラーニング界のムドーはやはりAlexNetですかね。

ブログ第二回で紹介してから、多層化、ReLU、コンボリューション、マックスプーリングと積み上げてきましたが、それも大詰め、今回はソフトマックス層について学んでいきます。
ソフトマックスはドラクエで言うとチャモロといったところでしょうか。

最終層をSigmoid関数にする際の課題

これまで、中間層はReLU、最終層はSigmoid関数を活性化関数に用いていました。
これまでやってきた、船と飛行機を見分ける問題だと、最終層に二つのニューロンを用意し、一つ目の出力が二つ目の出力より大きければ船、そうでなければ飛行機というように推論を行います。
つまり、大事なのは一つ目のニューロンと二つ目のニューロンの値の差ということになります。
理想的には、船の画像を入れたら、一つ目のニューロンの出力が1でもう片方が0、飛行機の画像を入れたらその逆ということになります。
そのため、船の画像を入れたら(1,0)、飛行機の画像を入れたら(0,1)を正解として学習させていました。

しかし、一つ目と二つ目のニューロンの差が重要ということなら厳密にいえば、(1,0)と(0,1)に近づけることに合理的でない場面も出てきます。

例えば、ある船の画像を入れたら、(0.9, 0.6)という値が出たとします。
二つのニューロンの値の差が0.3あるのである程度分離できていそうです。
では、(0.55, 0.40)という値だったらどうでしょう。
差は0.15で先ほどの半分なので、もう少し差がつくように学習したいですよね。
しかし、(1,0)からの二乗誤差はそれぞれ0.37, 0.36なのでどちらかというと(0.9, 0.6)のほうが誤差が大きい状態になります。
つまり、ニューラルネットから見ると、どちらかというと(0.9, 0.6)を(1,0)に近づける方が優先度が高いわけです。
※正しくは、誤差と優先度が比例するわけではないですがわかりやすさのため。

ソフトマックス関数

ソフトマックス関数はmax関数、つまり最大値のものは1、それ以外は0と似たような挙動を示しつつ微分可能な関数です。
ある種のノーマライズですが、単純に足して割るだけではなく、指数関数をかませているので、最大値に対してある程度小さい値が無視されるようになります。

先ほどの例にソフトマックス関数をかぶせると差がビビッドになります。
(0.9, 0.6) は(0.57, 0.425)に(0.55, 0.4)は(0.53, 0.46)になります。
二乗誤差も逆転します。
Sigmoid関数をかぶせた場合は(0.71, 0.64), (0.63, 0.59)となり、二乗誤差は逆転しません。

なお、Sigmoidは一つの値を入れたら一つ値が返ってくる関数でしたが、こちらはベクトルを入力としてベクトルが返ってきます。

ソフトマックス関数についてはこちらを参考にさせていただきました。
mathtrain.jp

ソフトマックス関数をお手軽に試せるwebページもありました。
keisan.casio.jp

ソフトマックスは意外と難しい

ソフトマックスは一般的なニューラルネットライブラリでは全結合層の関数の一つとして使用することができます。
しかし、実装に向けて考えていくと、SigmoidやReLUなどと大きく違う部分が出てくるので、今回は数式から考え直してみたいと思います。

１．スカラー入力とベクトル入力の差

SigmoidやReLUはスカラー入力でしたが、ソフトマックスはベクトル入力です。
なので、関数の形が変わります。
微分も変わります。入力のN個の変数で出力のN個の変数を微分できるのでN×Nの行列になります。

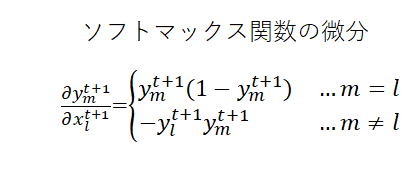
２．微分の連鎖律でΣが消えない

バックプロパゲーションは二乗誤差を重みで偏微分した値を求める必要があります。
偏微分が一発でできないときは、中間的な変数で微分してさらにそれを微分したい変数で微分して和をとる連鎖律が用いられます。

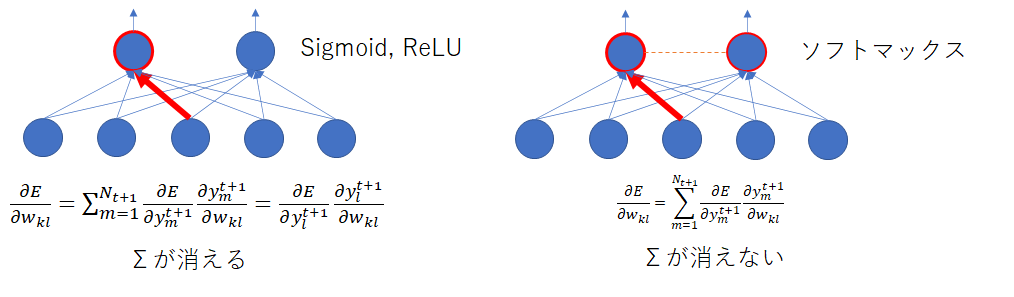
今までは $w_{kl}$ は $y_l$ だけに関係していたので、 $y_l$ が出てこない項は微分値がゼロになり、自動的にΣが外れました。
一方、ソフトマックスでは $w_{kl}$ によって $y_l$ 以外も変動するようになるため、Σが外れなくなります。

１．２．に注意して式変形するとこんな感じですかね。
数式は手を動かしながらじゃないと分からないと思うので、飛ばして読んでも大丈夫です。

f:id:kasuya_ug:20200601173151p:plain:w300
f:id:kasuya_ug:20200601173305p:plain:w350

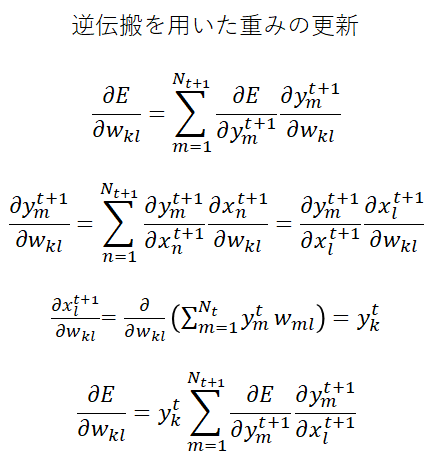
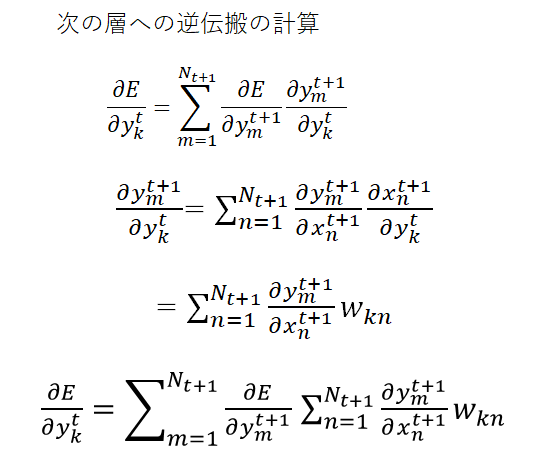
私が手作業で計算したので間違っていたら教えてください。

実装

いつも通りC#で実装して試していきます。
Sigmoid, ReLU等

        public override void CalcBackPropagation(NeuralImage dEdy)
        {
            var delta = new double[numNeuron];
            //Σが消えるのでここで一回だけ計算
            for (var i = 0; i < numNeuron; i++)
            {
                delta[i] = dEdy.data[0][0, i] * differentialFunc(states.data[0][0, i], T);
            }

            for (var p = 0; p < underPlane; p++)
            {
                for (var i = 0; i < underHeight; i++)
                {
                    for (var j = 0; j < underWidth; j++)
                    {
                        for (var k = 0; k < numNeuron; k++)
                        {
                            var d = delta[k] * inputs.data[p][i, j];
                            deltaWeights[p][i, j, k] += d;
                        }
                    }
                }
            }

            dEdyNext = new double[underPlane][,];

            for (var p = 0; p < underPlane; p++)
            {
                dEdyNext[p] = new double[underHeight, underWidth];
                for (var i = 0; i < underHeight; i++)
                {
                    for (var j = 0; j < underWidth; j++)
                    {
                        dEdyNext[p][i, j] = 0;
                        for (var k = 0; k < numNeuron; k++)
                        {
                            dEdyNext[p][i, j] += dEdy.data[0][0, k] * weights[p][i, j, k] * differentialFunc(states.data[0][0, k], T);
                        }
                    }
                }
            }
        }

ソフトマックス

        public override void CalcBackPropagation(NeuralImage dEdy)
        {
            var dydx = NeuralFunc.DSoftMax(outputArray);//微分する入力値がベクトルで、結果が行列

            for (var p = 0; p < underPlane; p++)
            {
                for (var i = 0; i < underHeight; i++)
                {
                    for (var j = 0; j < underWidth; j++)
                    {
                        for (var k = 0; k < numNeuron; k++)
                        {
                            var delta = 0.0;
                            //Σが消えないのでループの中でループして計算
                            for (var m = 0; m < numNeuron; m++)
                            {
                                delta = dEdy.data[0][0, m] * dydx[k,m];
                            }
                            var d = delta * inputs.data[p][i, j];
                            deltaWeights[p][i, j, k] += d;
                        }
                    }
                }
            }

            dEdyNext = new double[underPlane][,];

            for (var p = 0; p < underPlane; p++)
            {
                dEdyNext[p] = new double[underHeight, underWidth];
                for (var i = 0; i < underHeight; i++)
                {
                    for (var j = 0; j < underWidth; j++)
                    {
                        dEdyNext[p][i, j] = 0;
                        for (var k = 0; k < numNeuron; k++)
                        {
                           //ここもループが増える
                            var sigma = 0.0;
                            for (var m = 0; m < numNeuron; m++)
                            {
                                sigma += weights[p][i, j, m] * dydx[m, k];
                            }

                            dEdyNext[p][i, j] += dEdy.data[0][0, k] * sigma;
                        }
                    }
                }
            }
        }

プログラムは結果として今までループの外側にあった部分が中に移動しただけで、大きな変更はありませんでした。
ループの多重度は増えましたが、今のところ最終層で限られたニューロン数でしか使用されないので、速度低下の原因にはなっていないです。

実験

いつも通り、4500枚ずつの船と飛行機のCifar10の画像を学習させ、500枚でテストします。ネットワーク構造も前回と変えずに実施しています。

結果は・・・また誤差かなというレベルで上がりました。
前回、87.6%だったところから最大88.0%になりました。

蛇足ですが、DeepLearningは学習に時間がかかるので結構ちゃんとした評価難しいですよね。
一日かかるような学習の場合は10回実験して既存手法と勝負しようと思っても10日かかってしまうわけで。
また、10回やったとして平均をとるだけでは、たまたま一つの初期値が悪くて足を引っ張っただけで全体的にはいいということもあるし、10回に一回ぐらいは結構いい学習ができるけどそれ以外はそんなに良くないみたいなピーキーな学習が売りのネットワーク構造もありえそうですよね。

ブログなので厳密な評価はしていないですが、これからも嘘の無いようにはしていきたいと思います。

もうちょっと実験

さて、ソフトマックスは(1, 0)にかけると(0.73, 0.27)が出てきます。
(5, 0)だと(0.993, 0.007)です。
なので(1,0)が出るように学習すると、結構下の層に大きい数を出すことが要求されて、
学習が発散してしまわないか心配になります。
(0.7, 0.3)になるように学習したほうがいいのか、(0.9, 0.1)になるように学習したほうがいいのか。
でも実際は杞憂で、(1, 0)を正解として学習するのが一番良い結果になりました。
f:id:kasuya_ug:20200604134927p:plain