こんにちは、ニューラルネット老人こと糟谷勇児です。
今回はGlobal Average Poolingを学んでいきます。
Global Average Pooling層を入れると全結合層が要らないらしいぞと聞いて、思いは複雑です。
というのも、私が学生の頃に学んだバックプロパゲーションを用いたパーセプトロンは全結合層をSigmoid関数でつないだものでした。今や、SigmoidはReLUとSoftmaxになり、全結合層はコンボリューション層とPooling層だけになりと、ついに当時の面影がゼロになってしまうからです。とはいえ、当時のパーセプトロンは精度がそんなに良くなかったので、全結合層がなくなると、まあ精度も上がるんだろうななんて思ってしまうのもやはり複雑な思いです。
そのうち、バックプロパゲーションもなくなるのかもしれないですね。
ところでバックプロパゲーションを誤差逆伝搬法と日本語で言うのはなんでなんですかね。
微分の計算式が一つ上の層の漸化式で書けるというだけで誤差自体が伝搬しているわけではないと思うんですが。
まあ、それは置いておいて、Global Average Poolingを学んでいきます。
Global Average Poolingとは
qiita.com
こちらのブログの解説のほうが詳しくて恐縮ですが、一つ下の層で作られた出力平面を、その平面ごとに平均値をとる層ということのようです。
512平面の特徴マップが下の層から来ていたら、512次元のベクトルに変換されるということですね。
いくらなんでもそんな単純でいいんでしょうか。
効果としてはメモリ使用量の低減が挙げられます。例えばVGGの全結合層は25088×4096=102,764,544 個のパラメーターを持っていますが、これが512個のパラメーターになれば単純計算で20万分の1のパラメーター数になります。
一方速度に対する効果は限定的なのかなと思ったりします。
VGGのblock4のコンボリューション層では512×512×3×3×56×56=7,398,752,256回の掛け算、足し算が必要になるので、全結合層とは一桁以上計算量が違いますし、層の数も数倍あるので、150の計算量が149になるというレベルなのかなと。
また、精度も上がるとされています。本当でしょうか。
Global Average Pooling層のバックプロパゲーションの計算
Global Average Pooling層の計算は処理がシンプルなため、計算も簡単です。言ってしまえば、ある一つの平面に対して、出力ニューロンが一つ、重みが下の層のニューロン数分の1の全結合層と同じになります。
それなら、ニューロンを層の数と同じにした全結合層でも大体同じと思ってしまいますが、どうなんですかね。実験してみたいところです。
今回もバックプロパゲーションの数式を図示しておきます。
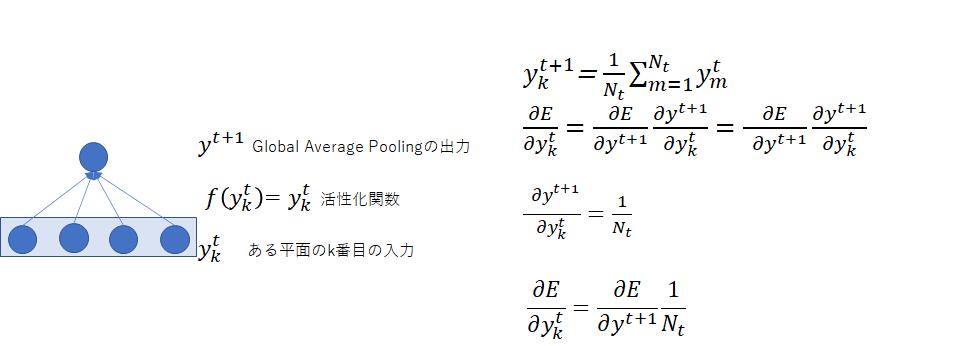
ちなみに、この数式はパワーポイントで書いています。私が卒論を書いていた当時は、パワポには数式エディタがなかったので、頑張ってワードで書いていましたが、大変だったので、修士はニューラルネットの研究をやめて、手書き数式エディタの研究に移行しました。
Global Average Pooling層の実装
私の実装では、層はLayerというクラスを継承して必要な部分のみを書き足すことで実装します。今回は次の出力のために平均を取るところも簡単なのでほとんど事務的にoverrideする感じになります。
また、バックプロパゲーションの計算は下記のような感じになります。次の層へはnで割った前の層の微分値を入れておくだけなので簡単ですね。ボトルネックにもならない箇所なので高速化は不要です。これだけ見てもなんのこっちゃという感じではありますが、ループで割り算するだけということが分かってもらえればと思います。
public override void CalcBackPropagation(NeuralImage dEdy) { var n = underHeight * underWidth; for (var i = 0; i < underPlane; i++) { dEdyNext[i] = new double[underHeight,underWidth]; for (var y = 0; y < underHeight; y++) { for (var x = 0; x < underWidth; x++) { dEdyNext[i][y,x] = dEdy.data[0][0, i] / n; } } } }
実験
前回作ったネットワークの全結合層をGlobal Average Pooling層に変えてみます。
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- MaxPooling層 サイズ3×3 ストライド2
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- MaxPooling層 サイズ3×3 ストライド2
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- 全結合層(ReLU) ニューロン数120
- 全結合層(ReLU) ニューロン数84
- ソフトマックス層 ニューロン数2
これを
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- MaxPooling層 サイズ3×3 ストライド2
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- MaxPooling層 サイズ3×3 ストライド2
- コンボリューション層 フィルタ数20 サイズ 3×3 ストライド1
- 活性化層(ReLU)
- Global Average Pooling
- ソフトマックス層 ニューロン数2
こう変えます。ただ、オリジナルのVGGは512平面の特徴マップがコンボリューション層で生成さるので、Global Average Poolingしても512次元の情報が残るのですが、こちらは20平面ですので20次元に圧縮されてしまいます。本当にこれでうまくいくのでしょうか。
いつものように500エポックほど学習させてみます。実験に使用するデータは今まで同様Cifar10の船と飛行機の画像5000枚ずつをデータオーギュメンテーションしたものとしました。
buildersbox.corp-sansan.com
パラメーターは前回と同じものを用いました。
buildersbox.corp-sansan.com

あれ、誤差が0.18までしか減っていない。全結合層があるときは0.01以下になるのに。精度も90%に届いていないですね。
でもGlobal Average Poolingはまだ学習をあきらめていないのかもしれない。
5000エポックまで学習してみましょう。

誤差は下がってきましたが、精度としては90%を超えないぐらいで推移し、最大でも89.3%にとどまりました。
おそらく、今回使用したニューラルネットでは特徴マップの平面数も、層の数も足りなかったのではないかなと思います。
収束は遅く、精度もあまり高くなりませんでしたが、全結合層がなくなって非常に単純化され、中で何が起こっているのかは多少見えるようになった点はよかったかなと思います。
20平面ぐらいなら、このデータはなぜ認識ミスをしたのか?と疑問に思ったら、それに反応した平面をたどっていくと原因もわかってくるかもしれません。それが悪さしているとなれば手動プルーニングも可能ですしね。
とはいえ、Global Average Poolingの本当の実力も見てみたいので、次回以降でより平面数が多く、より層の数が多いニューラルネットでも試していみたいと思います。
次回は
さて、そろそろ、ソースコードがごっちゃりしてきたので、リファクタリングしていきたいのですが、
何の目的もなく整理するのも大変なのでソースコードをgithubに公開していこうと思います。
今回第12回ということは月一の連載で1年やってきたということですので、頑張った反面コードはスパゲッティ化しています。それを解きほぐしながらアップロードしていこうと思いますので、どなたかレビューをお待ちしています。
▼本シリーズのほかの記事はこちら