こんにちは、ディープラーニング老人こと糟谷です。
前回は2006年の技術を追実験しましたが、まだ13年の隔たりがあります。今日も隔たりを埋めていきたいと思います。
長らく冬の時代が続いていたニューラルネットワークであるが、2006年にジェフリー・ヒントンによってスタックドオートエンコーダなど多層にネットワークを積み重ねる手法が提唱され、さらに2012年には物体の認識率を競うILSVRCにおいてジェフリー・ヒントン率いるトロント大学のチームがディープラーニングによって従来の手法(エラー率26%)に比べてエラー率17%と実に10%もの劇的な進歩を遂げたことが機械学習の研究者らに衝撃を与えた。
引用:「ディープラーニング」『フリー百科事典 ウィキペディア日本語版』より。(最終日付 2019年8月15日 (木) 21:34)
ということで、今回は2012年のAlexNetについて学んでいきたいと思います。
AlexNetについての論文はここから読むことができます。
https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
2006年のAutoEncoderは、層を重ねることで3層のニューラルネット以上の性能を出すことを示したものの、画像処理の応用においては当時流行っていた、SURF特徴量を用いた方法ほどの実用性はなく、私の周りではあまり話題になりませんでした。
一方の2012年のAlexNetは実用性を兼ね備え、一世を風靡しました。私も出張中に海外の研究者から、ニューラルネットが現状の最高の精度を出していると聞きジョークなのかと疑ったものでした。
AlexNetは様々な特徴があります。
・活性化関数ReLU
・Max Pooling
・GPUの活用
・Data Augmentation
・Dropout
どれも今も使われている技術ですが、一度に理解するのは大変なので、今回はReLUについて実験してみます。
ReLU
ニューラルネットワークの活性化関数は生物のニューロンの働きを模してヘビサイドの階段関数であらわされていました。これはニューロンがシナプスから一定以上の刺激を受けると発火するということを模したものです。しかし、階段関数は微分可能なすべての点で微分係数が0のため、微分を用いた最適化に不向きでした。
そこで、微分可能なSigmoid関数が一般的に使用されるようになりました。
ReLUはSigmoid関数とは異なり、階段状ではなく、しかもx=0において、右微分係数と左微分係数が異なる、微分可能でない関数です。脳の仕組みからも数学的な美しさからも一歩進んで実用性に特化したような印象があります。
ReLUについては2010年のこちらの論文にも記載されています。
https://www.cs.toronto.edu/~fritz/absps/reluICML.pdf
ReLUのメリットとしては勾配が消失しないこと、スパースになることがしばしば挙げられます。
Sigmoid関数は層を重ねるたびに勾配に0~1の値が掛け算されていくので、下の層に届く前に勾配の値が小さくなりすぎ、学習が遅くなってしまうというのです。
本当でしょうか。
実験
さて、前回作ったAutoEncoderをReLUとSigmoidで実験してみました。
実験は前回から引き続きC#で独自のニューラルネット実装を作って行っています。
実験1:勾配の絶対値と重みがゼロになったシナプスの比率
5層のAutoEncoderと7層のAutoEncoderを積み重ねずに一気に上から学習してみました。
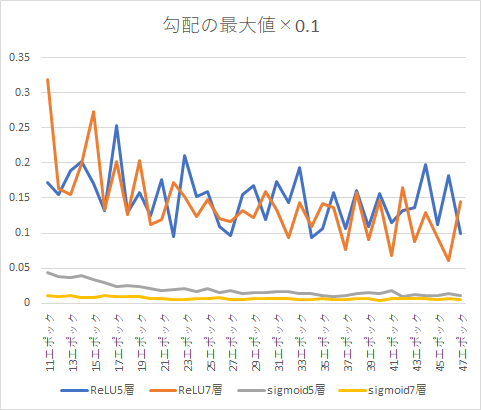
まずは学習時の勾配を比較してみます。
確かに、ReLUは層を増やしても勾配の値があまり変わらないのに対して、Sigmoidでは層を増やすとどんどん小さくなっていきます。
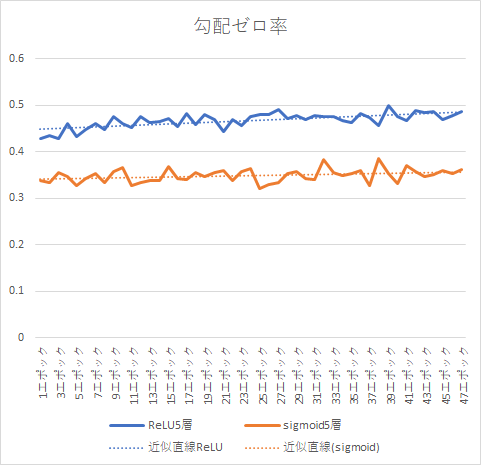
次に勾配が0になったシナプスの数を比較します。
ReLUでは勾配が0のシナプスが元からSigmoidより多いですが、その数はどんどん増加していきます。
一度、勾配がなくなったシナプスはその後、基本的に復活しないので、どんどんスパースになっていきます。
今回は単純にfor文で勾配を計算していますが、行列計算で行えば、スパースな行列の掛け算は高速に行えるので、学習が早く行えます。
実験2 トータルな学習ではどちらが良いのか
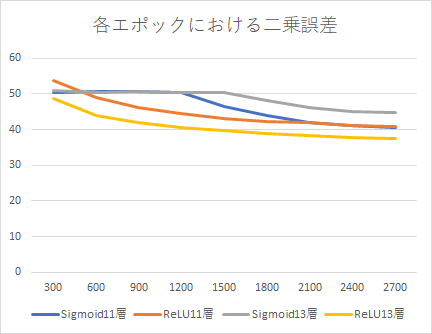
図に実際に学習した際の、二乗誤差の推移を示します。
11層のAutoEncoderではSigmoid関数でもReLUでも3000回学習した際の二乗誤差は変わりません。一方13層ではReLLUのほうが低い誤差を得られました。
多層のニューラルネットではReLUのほうが有利な様子です。ちなみに7層まではSigmoidのほうが誤差が小さくなります。
多層や複雑なニューラルネットではReLU、層が薄い場合はSigmoidという使い分けがよさそうです。
ReLUの難しかったところ
正直、実際にやってみる前はもっとReLUは万能なのかなと思っていました。
一方で実装してみると難しい面もわかってきました。
1.初期値の与え方によってはうまく学習できない
Sigmoid関数は最大で1ですが、ReLUはどこまでも大きくなるので、平均0.5の重みでニューロンが100あれば次の層に50の強さ、その次の層には5000の強さになって届きます。そのため、初期値はニューロンの数によって決めなければいけません。
こちらのブログによると、その層のニューロンの数をnとすると、分散が、平均が0の正規分布にするのが良いようです。
https://to-kei.net/neural-network/initial_value/
2.学習率を調整しないと一気にシナプスの重みが負になってしまい、学習が止まってしまう
Sigmoid関数はどこまででも勾配がありますが、ReLUは0を下回ると勾配がなくなってしまい、学習が行われなくなってしまいます。
そのため、学習率が大きすぎると一気に重みが負になってしまい、すべてのニューロンが活動しなくなり、学習が止まってしまいます。
今回は勾配の絶対値が、の1/100を上回ったら強制的に補正をするようにしました。
勾配消失問題ってなんだ?
確かにReLUは勾配の絶対値が層を増やしても小さくならないという特徴があります。
しかし、Sigmoidの課題が、勾配の絶対値が小さくなることだとするなら、下の層に行くほど学習率を増やしてあげればいいだけです。おそらくですが、単に小さくなるだけでなく、Sigmoid関数の場合、下の層の重みの影響が複雑かつ大きく変化しない関数になってしまい学習がうまくできなくなっているのではと想像します。
次回はそのあたりを検証していきたいと思います。