Metalシェーダーで形状のアニメーション

技術本部の堤です。弊社には「Geek Seek Workshop」という社内勉強会を支援する制度がありまして、かなり活発に利用されています。私もその制度を利用して、もう1名の同僚と「リアルタイムグラフィックスの数学 - GLSLではじめるシェーダプログラミング」という書籍を一緒に読み進めていました。

gihyo.jp

本書はリアルタイムグラフィックスの解説書です。基礎から積み上げていくので、勉強会を続けていくうちに、以前だったらおまじないのようにしか見えなかった次のようなシェーダーのコードが理解できるようになってきました。

本書を読み進めていく中でとくに感動したのが、SDFと呼ばれる関数を用いて形状を描画することで、形状同士の結合や形状間のモーフィングといった形状の操作を非常にシンプルな演算で行えるという点です。

たとえば次のようなモーフィングは、なんとmin関数ひとつで実現されています。

この感動と学びをどこかで発信しよう、ということで私はiOSエンジニアなのでGLSLの書籍のサンプルをMetalシェーダー（Metal Shader Language / MSL）に移植し、

github.com

Yakatabune.swift という海外からのエンジニアも多く参加した英語ベースのSwift/iOSのイベントでLTしてきました。

www.docswell.com

以下、上の発表スライドを記事として再構成したものになります。

「形状のアニメーション」の例

「形状のアニメーション」をどう実現するか？

各フレームにおける形状を定義して連番画像を表示する？

→大変すぎる

ベクター画像のように形状を数式化あるいはコード化して、時間経過に応じて変化させる？

→これもなかなか難しい

そんなことしなくても関数ひとつで実現できてしまいます。

それをこれから解説します。

形状を距離で表現する

Signed Distance Function (SDF)

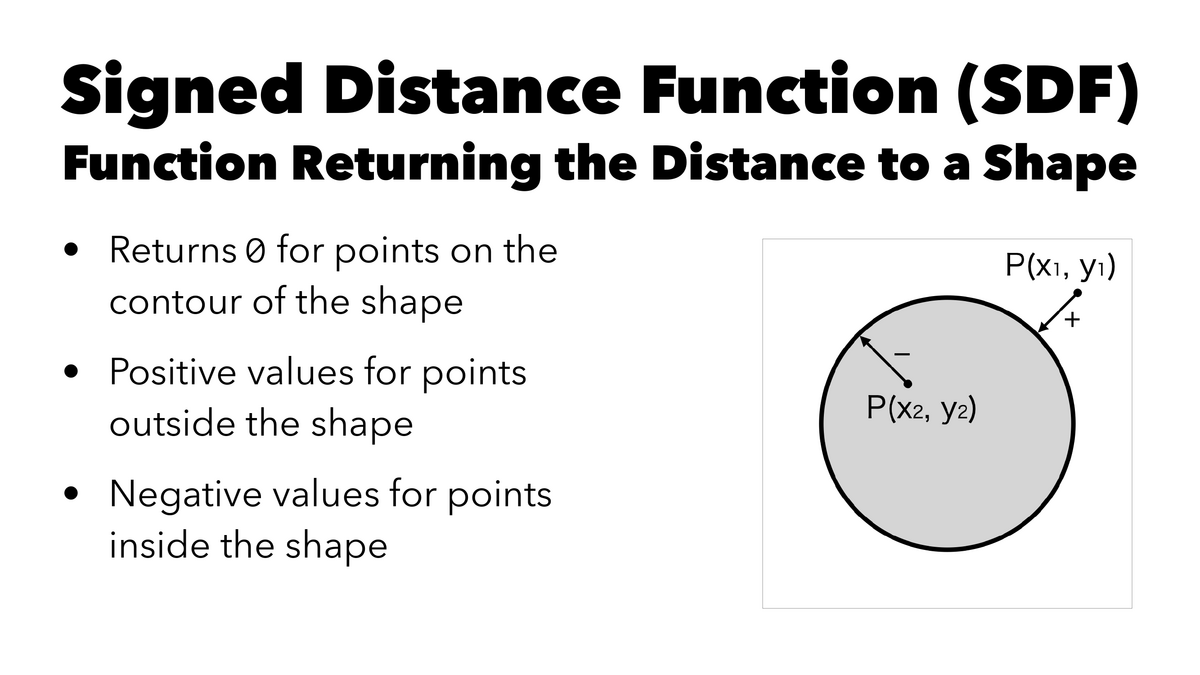
SDF: 図形との距離を返す関数

図形の輪郭線上にある点では値が 0
外側ではプラスの値
内側ではマイナスの値

円のSDF

この「円のSDF」の実装はMetal Shader Language（MSL）では次のようになります。

float circleSDF(float2 p, float2 c, float r) {
    return length(p - c) - r;
}

この円のSDFを描画するMSL全体のコードは次のようになります。

float circleSDF(float2 p, float2 c, float r){
    return length(p - c) - r;
}

float contour(float v) {
    return step(abs(v), 0.008);
}

[[ stitchable ]] half4 circleShader(float2 position,
                                    half4 color,
                                    float4 boundingRect)
{
    float2 p = (position.xy * 2.0 - boundingRect.zw) / min(boundingRect.z, boundingRect.w);

    half3 rgb = contour(circleSDF(p, float2(0.0), 0.9));
    return half4(rgb, 1);
}

サンプルでは circleShader.metal

球のSDF

球のSDFは、円のSDFと引数の型が float2 （2次元）から float3 （3次元）に変わるだけです。

球のSDFの描画にはカメラ、ライティング、レイキャスティング・レイマーチングといった3Dグラフィックスの知識が必要になってきますが、LTでは時間が足りないので割愛しました。書籍では順を追って非常にわかりやすく解説されています。

Metal SDF Examples では mathShader_8_6.metal 参照。

ここまでのまとめ

形状を「距離で」表すSDFについて解説しました。

SDF形状のコントロール

ここがこのLTで一番伝えたいパートです。

SDFを用いることで、2Dであれ3Dであれ、形状を距離というひとつの数値で表現 できてしまいます。

形状の結合

min(d1, d2) 関数ひとつでSDFの和集合を計算できます。

半径の違う2つの円のSDFの和集合を min 関数で結合する例を示します：

// Circle SDF 1
float d1 = circleSDF(p, float2(0,  0.5), 0.9);
// Circle SDF 2
float d2 = circleSDF(p, float2(0, -0.5), 0.5);
// The union of SDFs
float u = min(d1, d2);

→SDFの和集合を取ることで、元のSDF形状を結合した形状が得られます。

min 関数を用いて形状を結合する別の例：

float d = 1.0;
for (float i = 0.0; i < 6.0; i++) {
    // 円周上に球を配置（球の中心座標を決めている）
    float3 cent = float3(cos(PI * i / 3.0), 
                         sin(PI * i / 3.0),
                         0.0);
    // 和集合を取っていく
    d = min(d, sphereSDF(p, cent, 0.2));
}

→6つの球を1つのSDFで表現できます。

モーフィング

mix(x, y, a) 関数で形状同士のモーフィングが可能になります。

mix関数は2つの値 x, y の間を a の値に応じて補間する関数で、数式としては以下で表されます。

x + (y – x) * a

たとえば x, y を次のようなSDF形状とし、

x: 1つの球を表すSDF
y: 6つの球を表すSDF

a を次のように経過時間に応じて 0.0 ~ 1.0 を周期的に繰り返すようにすることで、

float a = abs(mod(time, 2.0) - 1.0);

次のようなモーフィングが実現できます。

Metal SDF Examples では mathShader_9_2.metal 参照。

滑らかな結合

滑らかにSDFが結合するようにつなぎ目が補間されたmin関数である smin という関数を次のように定義し、

// A min function that interpolates the junction for a smooth SDF union
float smin(float a, float b, float k) {
    float h = clamp(0.5 + 0.5 * (b - a) / k, 0.0, 1.0);
    return mix(b, a, h) - k * h * (1.0 - h);
}