こんにちは,DSOC R&Dグループ インターン生の吉田と申します.
2017年のサマーインターンに参加して以来,1年半程こちらでお世話になっておりますが,この春に就職を控えていることもあり、この度2月末で退社させていただくことになりました.従って,これが最初で最後のエントリーとなります.
大学では主に時系列のセンサデータ等を扱った研究を行っていますが,インターンでは名刺のネットワーク分析に携わらさせていただきました.大学の研究とは性質の異なるデータの分析は非常に刺激的であり,また大変興味深かったです.
本稿では,これからネットワーク分析を始める人向けに,インターンを通じて学んだネットワークの分析手法の基礎指標を紹介していきます.ただ紹介してもつまらないので,関東地方の路線図データを用いて,その特徴を様々な指標毎に分析していきます.なお,本稿の分析は全てpythonライブラリのnetworkxを用いて行いました.
ネットワークの全体の特徴を表す指標
ネットワーク分析には,実に様々な指標が存在します.分析を始めた頃は(今でもですが)各指標がそれぞれ何を表しているのか混乱することが多かったです.ここではまず,ネットワークの全体の特徴を表す,基本的な指標とその意味について見ていきます.
密度(density)
ネットワーク分析における密度\(density\)は以下の式で定義されます.\[density = \frac{m}{n(n-1)/2}\ =\frac{2m}{n(n-1)}\]
ただし,\(n\) はネットワーク中のノードの総数で,\(m\)はネットワーク中のエッジの総数です.この式は,張ることの出来るエッジ数に対する、実際のエッジ数の比率を表しています.
「密度」というからには,人的ネットワークなら密度が高い程噂話の伝達速度は早そうですし,電車の路線ネットワークなら密度が高い程各駅へのアクセスは良さそうな印象を受けます.分析を始めた時の吉田少年は,この式を見てネットワークの密度について分かった気でいましたが,この「密度」の定義が自分の想像していたような指標ではないことをすぐに思い知ります.
下の図は,東京都,神奈川県,千葉県,埼玉県,茨城県の各県の電車路線図の密度を示しています.



最短経路長(shortest path length)
最短経路長とは,任意のノードから任意のノードまで到達するのに必要な最低ステップ数のことを言います.各都道府県ごとに,全ての駅の組み合わせについて最短経路長を算出し,その平均を取ることで,各駅へのアクセスしやすさを直接的に求めることができます.これをネットワークの平均経路長と言います.平均経路長が短いほど,任意の駅へのアクセスが容易になると考えられます.
実際,各県の路線図の平均経路長は以下のようになりました.

クラスター係数(Clustering Coefficient)
あるノードの近隣ノード同士がリンク関係にある場合,ネットワーク中に三角形のサイクルが現れます.具体的には,ノードAがノードBとノードCのどちらにも繋がっており,さらにノードBとノードCも繋がっている時,三角形ABCが出現します.このような三角形(クラスター)を多く含むネットワークは「クラスター性が高い」と表現されます.クラスター係数とはクラスター性を定量的に測る指標であり,任意のノード\(i\)のクラスター係数\(C_i\)は、ノード\(i\)のエッジから作成可能な三角形のうち、実際の三角形の数の割合で定義できます。
\[C_i = \frac{ノードiを含む三角形の数}{k_i(k_i-1)/2}\]
ただし,\(k_i\)はノード\(i\)の次数(エッジ数)を表しています.また,ネットワーク全体のクラスター係数\(C\)は,全ノードのクラスター係数の平均値として得られます.
\[C = \frac{1}{n} \sum_{i=1}^{n}C_i\]
以下に,各都道府県の路線ネットワークのクラスター係数を示します.

ネットワークの中心性
中心性の種類
ネットワークにおけるは中心性とは,各ノードの重要度を測るための指標です.しかし,中心性には実に様々な定義が存在するので,ここでは代表的なものを紹介します.次数中心性 (Degree Centrality)
ノード \(i\) の次数中心性 \(DC_i\) はノード \(i\) の次数 \(k_i\) そのものです.つまり,ノードのリンク数が多いほど中心性が高くなります.networkx では,次数を自分以外のノードの数 \((n-1)\) で割って正規化したものを使っています.\[DC_i = \frac{k_i}{n-1}\]
近接中心性 (Closeness Centrality)
ノード \(i\) の近接中心性 \(CC_i\) は,自分以外の全てのノードから自分までの最短経路長の合計値が小さいほど大きくなります.つまり,他のノードから見てアクセスしやすい位置にいるノードの中心性が高くなります.式としては以下で表されます.\[CC_i = \frac{n-1}{\sum_{j=1}^{n-1}d(i, j)}\]
ただし, \(d(i, j)\) はノード \(i\) とノード \(j\) の最短経路長を示しています.
媒介中心性 (betweenness centrality)
ノード \(i\) の媒介中心性 \(BC_i\) は,任意の2つのノード \((s, t)\) の最短経路にノード \(i\) が含まれる確率で表されます.\[BC_i =\sum_{s,t \in V}\frac{\sigma(s, t|i)}{\sigma(s, t)}\]
\(V\) はノードの集合, \(\sigma(s, t)\) はノード \((s, t)\) 間の最短経路の数(最短経路は一つとは限らない),\(\sigma(s, t|i)\) はノード \((s, t)\) 間の最短経路の内ノード \(i\) が含まれている経路の数です.
PageRank
PageRankは以下の3つのアイデアを基礎としています.- ノード \(i\) の中心性は,沢山のノードからリンクが貼られている程(=次数が高い程)高くなる
- ノード \(i\) がリンクしているノード \(j\) の中心性が高い程,ノード \(i\) の中心性も高くなる
- ノード \(i\) がリンクしているノード \(j\) の中心性の価値は,ノード \(j\) の次数が低い程高い
この3点をベースにした,ノード \(i\) のPageRank \(PR_i\) は以下の式で定義されます.
\[PR_i =(1-d) + d\sum_{j \in V_i}\frac{PR_j}{k_j}\]
ただし,\(V_i\) はノード \(i\) がリンクしているノードの集合であり,\(d\) はダンピング・ファクターと呼ばれるハイパーパラメータです.定義式では,\(PR_j\) の合計を取ることで上記のアイデア1と2を回収し,また \(PR_j\) をノード \(j\) の次数 \(k_j\) で割ることでアイデア3を回収しています.
中心性の性質の違い
東京都の路線図データを用いて,東京都の各駅の中心性を計算してみました.どの中心性を用いるかは目的によって異なりますが,ここでは特に近接中心性とPageRankに注目して結果を見ていきます.まず,中心性が大きかった駅の上位10個を示します.いずれもの中心性でも新宿,東京,池袋,品川,渋谷などのハブ駅が上位に入っています.これらの駅が,東京都にとって重要な役割を果たしていることは,この結果からも明らかです.しかし一方で,一位こそいずれも新宿になっているものの,二位以下の順位は結構バラバラです.実際,2つの中心性の相関係数は 0.193 と小さい値になっており,中心性は定義によって大きくスコアが異なることがわかります.
| 順位 | 近接中心性 | PageRank |
|---|---|---|
| 1 | 新宿: 0.1436 | 新宿: 0.00621 |
| 2 | 四ツ谷: 0.1389 | 池袋: 0.00577 |
| 3 | 渋谷: 0.1376 | 品川: 0.00404 |
| 4 | 東京: 0.1362 | 拝島: 0.00397 |
| 5 | 品川: 0.1338 | 東京: 0.00394 |
| 6 | 吉祥寺: 0.1337 | 新橋: 0.00384 |
| 7 | 池袋: 0.1324 | 渋谷: 0.00379 |
| 8 | 中野: 0.1276 | 飯田橋: 0.0037 |
| 9 | 大久保: 0.1272 | 日暮里: 0.00368 |
| 10 | 初台: 0.1271 | 王子: 0.00367 |
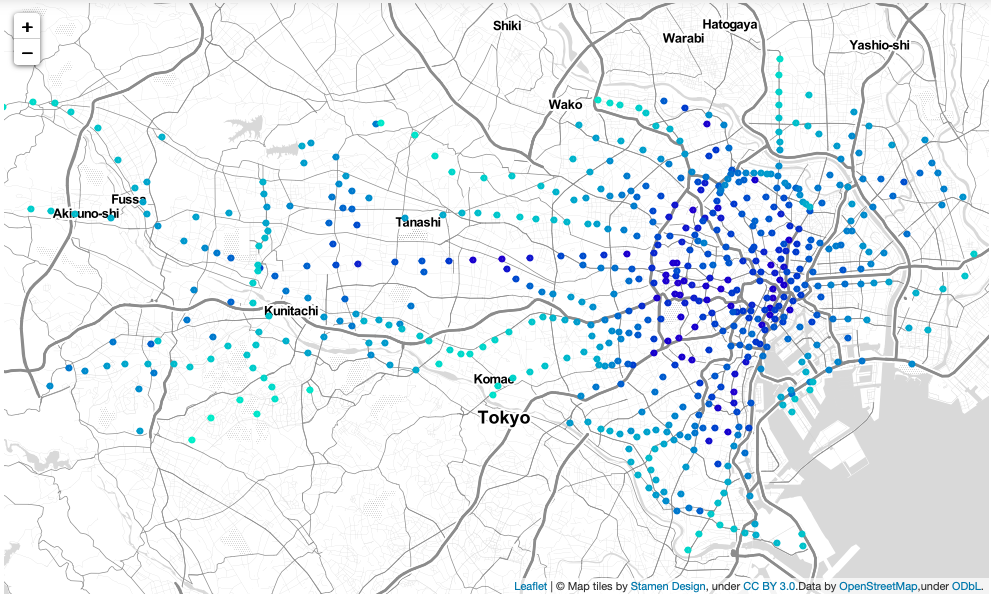
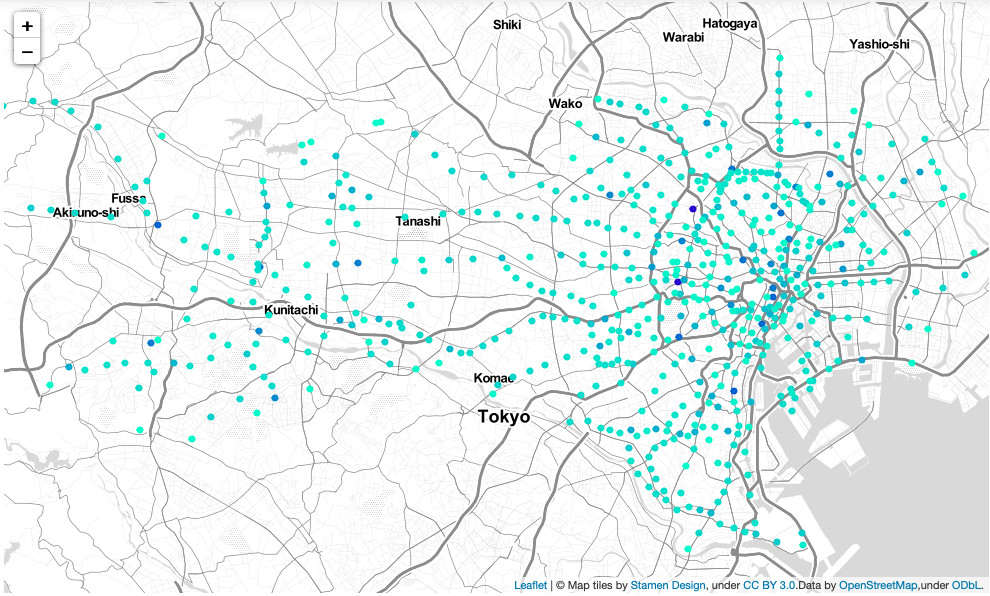
下図は,都内の駅を地図上にプロットしたものです.その駅の中心性が高い程,色が濃くなっています.
これらの図は,二つの中心性の性質の違いを良く表しています.近接中心性は,自分以外の全てのノードから自分までの最短経路長の合計値が小さいほど大きくなるので,東京駅や新宿駅などのハブ駅に近いほど中心性が高くなります.図においても,都心に近いほど中心性は高くなっており,郊外に行くほど中心性が低くなっているのが分かります.
一方PageRankの方は,地図上に中心性の高い駅が散在しています.前述したように,PageRankではノードの次数が大きいほど中心性が高くなりますが,東京駅や新宿駅などのハブ駅以外の駅の次数はほとんどが2なので,これらハブ駅の中心性のみが高くなっています.
因みに,今回用いたネットワークでは,PageRankと次数中心性の相関係数が 0.914 で,PageRankが次数に大きな影響を受けていることが分かります.
まとめ
ネットワーク理論における基本的な指標をまとめました.ネットワーク理論には本当に様々な指標が存在しており,例えば,単に「このネットワークがどのくらい密かを検証する」と言っても,その指標を密度\(density\),平均経路長,クラスター係数にするのかによって答えが変わってきます.また,中心性にも様々な定義が存在し,用いる定義によってノードの中心性も変化することを確認しました.当たり前ですが,重要なのは各指標の意味を理解して,臨機応変に使い分けることでしょう.
最後に
本稿ではインターンを通じて得たネットワークの基礎分析方法についてまとめましたが,インターン中に学んだことは多岐に渡り,ここに記したものはそのごく一部です.Sansan DSOC には多様な専門性を持っているメンバーが在籍しており,ネットワーク分析の知識はもちろんですが,それ以外にも自然言語処理や統計に関する知識,コーディングのスキル等,実に様々な知識を得ることが出来ました.元々,大学の研究とは性質の異なるデータに触れて,知見を広げたいと思ってインターンに応募しましたが,想像以上の収穫があり、大変刺激的な毎日を過ごすことができました.
*1:R. Albert and AL. Barabási“, Statistical mechanics of complex networks”, Rev. Mod. Phys., Vol. 74, 47-97 (2002)