
こんにちは.そして,あけましておめでとうございます. Sansan DSOC 研究開発部の黒木裕鷹です. 8月下旬からはじめたこの連載も,はやいもので第4回となりました. 結構な文量をそこそこのペースで書いているような気もしますが,仕事もちゃんとしているつもりです(笑)
さて,この連載では,自分の勉強・復習も兼ねて,ネットワークデータにまつわる統計解析を気の向くままに紹介しています. 前回の記事では,特に複雑ネットワークを中心として,1980から2000年代に盛んに開発されてきた手法を紹介しました. 今回からはいよいよ,ネットワークデータに対する深層学習 (Graph Neural Network; GNN) やノードの表現学習 (node embedding) を俯瞰していきたいと思います. ただし,少しボリュームが出てしまうのでさらに2回に分け,GNNの大部分は次回記事に回します.
それではやっていきます.
はじめに
深層学習は,特に画像や自然言語領域を中心とし,近年目覚ましい発展を遂げています. テーブルデータに対しては,LightGBM や XGBoost, CatBoost をはじめとした決定木系の勾配ブースティングが依然として猛威を振るっていますが,TabNet という,決定木のメリットをうまく取り入れたテーブルデータ用の深層学習モデルも出てきているようです. これらの領域に比べると,ネットワークデータに対する深層学習の適用は少し遅れていますが,それでもここ数年は非常に盛んに研究されています.
Tabnetに関しては,DSOC 研究員 斎藤の記事が分かりやすかったです.
深層学習の適用を難しくしていたのは,やはりネットワークの構造に由来するところが大きいと思います. その構造のために,テーブルデータのように独立性を仮定することは現実的ではありませんし,せっかく観測されているつながりの情報を利用しないのも勿体ないでしょう. 画像や系列も同じく構造をもったデータですが,これらの構造は格子状であり,前後の関係を考慮するような工夫が役に立ちます. CNNやRNNのように,その構造を積極的に利用する工夫は現在でも重要な技術要素になっています. ネットワークはこれらと異なり格子状にはなっておらず,また構造の特性もネットワークやドメインごとに異なるため,どのようにその構造を利用すべきかに課題があります.
初めてのネットワークデータの深層学習 (Graph Neural Network; GNN) は,Scarselli et al.(2005, 2008) で提案され,ノード単位のタスクとグラフ単位のタスク両方に対する手法が提案されました. グラフ単位のタスクとは,分子構造の分類のように,ネットワーク全体に対して属性を考えるタスクです. 一方でノード単位のタスクとは,ネットワークを構成する個々のノードに対して,分類や回帰などを行うタスクです.
ノード単位のタスクでは,ノードに付随する特徴量をそのまま使うことができますが,前述の通りノード同士が独立ではないため,何らかの方法で構造を利用しなければなりません. つまり,フィルタリングを行う必要があり,畳み込みやAttentionなど,現在までに様々なグラフフィルタが提案されています. 一方でグラフ単位のタスクでは,構造全体に対して特徴量を考える必要があるため,グラフフィルタに加えてグラフプーリングを行う必要があります. グラフプーリングも様々なものが提案されています.
これらGNNのフレームワークは,ノード(もしくはグラフ)に付随する情報を予測するための半教師あり (semi-supervised) 的なものですが,一方で教師なし (unsupervised) な手法も盛んに研究されてきました. 特に,ノードの特徴を連続空間で表現する node embedding の手法が実応用の面でも重要視され,様々な先行研究が存在します. 得られた埋め込み表現を後段のモデルにそのまま流用でき,一貫した end to end の学習ができなくなりますが,非常に使い勝手が良いメリットがあります.
GNNの様々なフィルタ,プーリングは次回の記事にまわし,ここからは node embedding を紹介していきます. オートエンコーダも次にまわします.
node embedding
node embedding は,個々のノードの特性を保持するように低次元ベクトルとして表現することを目的としており,一般的に下図のプロセスで行われます.
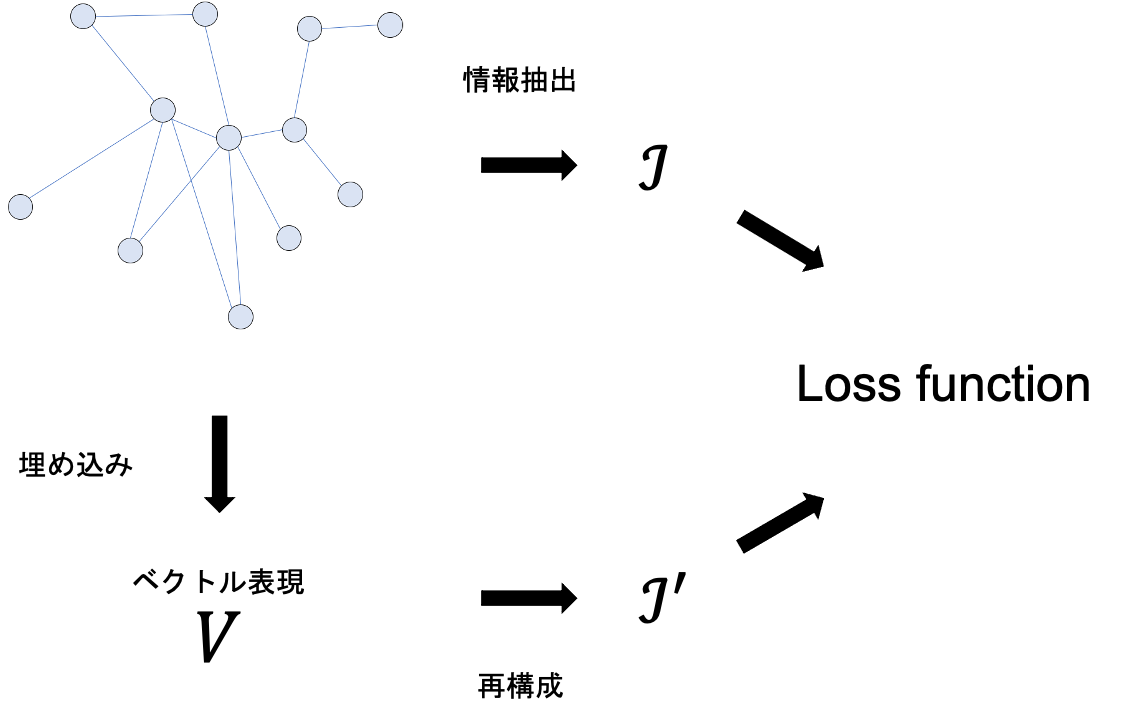
図から,情報抽出や loss function の設計には様々なものを考え得ることが分かるでしょう. つまり,様々な node embedding のモデルが提案されていますが,これらはノードの「どの特性」を「どのように」保持するか,という視点で整理することができます. まずノードの「特性」についてですが,多くのモデルはノードの近傍の情報(や接続)を保持するように設計されています. そのうえで,たとえば以下のようなバリエーションが提案されてきています.
- オーソドックスに,ノードの近傍(や接続)の情報を利用する.
- ノードがグラフ内で有する役割 (structural role) も利用する.
- ノードのコミュニティ情報を利用する.
次に,ノードの特性を「どのように」保持するかについてですが,ほとんどのモデルはもとのグラフを再構成できるように保持します. 技術的な詳細は多岐に渡りますが,その根底には「良い node embedding からは,もとのグラフの情報を再構成できる」という直感的なアイデアがあります. 次節では,上で挙げた項目について,代表的なモデルを簡単に紹介していきます.
ノードの近傍や接続の情報を利用するnode embedding
埋め込み表現を得るモデルとしては,自然言語処理の word2vec (Mikolov et al., 2013) が最も有名でしょう. node2vec は単語の系列から単語の埋め込み表現を得る手法ですが,グラフからもノードの共起情報を系列として抽出してくれば,word2vec を適用することができます. word2vec に関しては,分かりやすい日本語記事も多数存在するため,ここでは説明を割愛します. それでは,グラフからノードの共起情報はどのように抽出すれば良いでしょうか. その最も単純な手段として,ランダムウォークが考えられるでしょう. あるノードからスタートし,隣接するノードをランダムに遷移していくことで,ノードの系列が得られるということです. DeepWalk (Perozzi et al., 2014)は,ランダムウォークで得られたノードの系列からskip-gramを作成し,word2vec のアルゴリズムで学習を行うモデルです.
DeepWalk は word2vec (skip-gram) のアルゴリズムをそのまま適用するため,word2vec と同様に negative sampling や階層的ソフトマックスなど高速化の工夫を施すことができます. 実際,そこまで大規模なグラフでなければ,ラップトップなどでも現実的な時間で学習を行うことができます. また,DeepWalk はランダムウォークでノードの系列を得ますが,ここを工夫するアルゴリズムが DeepWalk 以降に多数提案されています.
ノードの接続の情報を利用するアルゴリズムとしては,他にも node2vec (Grover and Leskovec, 2016) や LINE (Tang et al., 2015) などが有名です. node2vec では,幅優先探索 (BFS) と深さ優先探索 (DFS) に基づく2つのランダムウォークを組み合わせ,偏りのあるランダムウォークによって系列を得ます. BFS で注目するノードの近傍を,DFS で遠くまでたどり着くような系列を得て,結果としてグラフ構造全体の特性を DeepWalk よりもうまく抽出しようという狙いがあります. 2種類のランダムウォークのバランスをうまく制御することで,グラフやタスクの種類に合わせた柔軟な埋め込みを考えることが重要です.
一方で LINE は,直接的な接続だけでなく2次の接続も積極的に利用する手法です. 1次と2次の接続での近さを別々に保持し,それぞれの埋め込みをマージすることができます. 色々なところでLINE(1), LINE(2), LINE(1+2) などを目にするのはこのことです. また,計算が非常に軽く,大規模グラフに適用することを前提に設計されているのも特徴です. DeepWalk のようにランダムウォークで系列を得ているわけではないのですが,実はランダムウォークの長さを1に設定するのと同じことをしていたりいします(細かい説明はまたいずれしたいとおもいます).
これら前述の node embedding は,行列因子分解の観点から再解釈できることが示されていたり(Qiu et al., 2018),理論的な解析の進んでいる手法でもあります.
ノードがグラフ内で有する役割 (structural role) も利用する node embedding
突然ですが,鉄道のネットワークを考えてみます. 新宿駅と梅田駅は東京と大阪で離れていますが,それぞれの地域内でハブとして,同じような役割を担っていることが予想されるでしょう. このように,あるノードがグラフ内で有する役割も積極的に保存するモデルが提案されています. その中でも,最も知られているであろう struc2vec (Ribeiro et al., 2017) をここでは紹介します.
直感的に,ノードの構造的役割を表す最もシンプルな特徴は次数でしょう. この直感に基づくと,同じような次数を持っているノード同士は,同じような役割を担っていると考えることができます. さらに,隣り合うノード同士もまた同じような次数をもっていれば,これらはさらに類似していると考えられ得ます. つまり,昇順(もしくは降順)に並び替えた近傍の次数系列を比較することで,直感的には構造的役割の類似性(のようなもの)が測れます.
struc2vec は,与えられたグラフから多層グラフを作りだすことで,このような階層的な類似性を埋め込もうとします.
このとき,第層のグラフを,
次の近傍との類似度(
次の近傍の次数系列同士がどのぐらい似ているか)を表すように作成します.
よって,より深い層のグラフほどより広い範囲の関係性を表現できることになります.
系列の類似度には,時系列の距離によく用いられる DTW (Dynamic Time Warping) を使うことが提案されていますが,系列同士を比較するものなら何でもよさそうです.
また,ここでは分かりやすくするために次数の例を紹介しましたが,その他中心性やクラスター係数など,構造の特徴を表すようなものなら何でもよさそうです.
系列を作成するランダムウォークでは,確率で同一層に留まり,確率
で異なる層にジャンプするようにします.
ハイパーパラメータ
を適切に選択することによって,ノードの接続だけでなく役割もうまく拾うことができます.
コミュニティ情報を利用する node embedding
現実のネットワークの多くでは,コミュニティ構造(ネットワークがより細かいクラスタに分けられるような構造)が観測されます. 単純な接続や近傍の構造だけでなく,コミュニティ構造も埋め込みに利用しようとする node embedding の研究もいくつか存在します. たとえば Wang et al. (2017)は,ノードの接続とコミュニティ構造の両方を保存するような行列分解に基づく手法, M-NMF (Modularized Nonnegative Matrix Factorization) を提案しています.
コミュニティ抽出の大半は modularity (Newman, 2006) の最適化よって行われます. そこで M-NMF では,ノードの表現がコミュニティの表現と似ていれば,そのノードはそのコミュニティに属する傾向が高いと仮定し, 補助的なコミュニティの表現行列を導入しています. このようにして学習したノードの表現は,ミクロな構造とコミュニティ構造の両方によって制約され,より多くの構造情報を含み,より識別性の高い埋め込み表現になるそうです.
おわりに
本記事では,主にノードの構造的情報を連続な低次元空間で近似する node embedding の統計的学習モデルを広く紹介しました. 本記事で扱えなかった node embedding のトピックとしては,二部グラフの埋め込みや時系列発展するグラフの埋め込み,ハイパーグラフの埋め込みなどがあります. 単純な node embedding でさえ,行列分解による埋め込み,古典的な次元削減手法による埋め込み,オートエンコーダを利用した埋め込みなど,扱えていないものが多く存在します. 範囲が広すぎてとても網羅できそうにありません(汗). node embedding についてはいくつかのサーベイ論文が出ており,より全体観を固めたい方はそちらを読むと良いでしょう(Hamilton et al., 2017; Goyal and Ferrara, 2018; Cai et al., 2018; Cui et al., 2018).
次回は,GCN や GAT などのグラフフィルタをはじめ,GNN を俯瞰的に紹介したいと思います. GNN については DSOC 研究員 吉村による記事も出ており,次回の記事は蛇足感もありますが,またよろしくお願いします.
参考文献
- Cai, H., Zheng, V. W., & Chang, K. C. C. (2018). A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Transactions on Knowledge and Data Engineering, 30(9), 1616-1637.
- Cui, P., Wang, X., Pei, J., & Zhu, W. (2018). A survey on network embedding. IEEE Transactions on Knowledge and Data Engineering, 31(5), 833-852.
- Gao, M., Chen, L., He, X., & Zhou, A. (2018). Bine: Bipartite network embedding. In The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, 715-724.
- Grover, A., & Leskovec, J. (2016). node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, 855-864.
- Goyal, P., & Ferrara, E. (2018). Graph embedding techniques, applications, and performance: A survey. Knowledge-Based Systems, 151, 78-94.
- Hamilton, W. L., Ying, R., & Leskovec, J. (2017). Representation learning on graphs: Methods and applications. arXiv preprint arXiv:1709.05584.
- Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. (2013). Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems, 26, 3111-3119.
- Newman, M. E. (2006). Modularity and community structure in networks. Proceedings of the national academy of sciences, 103(23), 8577-8582.
- Perozzi, B., Al-Rfou, R., & Skiena, S. (2014). Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, 701-710.
- Qiu, J., Dong, Y., Ma, H., Li, J., Wang, K., & Tang, J. (2018). Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, 459-467.
- Ribeiro, L. F., Saverese, P. H., & Figueiredo, D. R. (2017). struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, 385-394.
- Scarselli, F., Yong, S. L., Gori, M., Hagenbuchner, M., Tsoi, A. C., & Maggini, M. (2005). Graph neural networks for ranking web pages. In The 2005 IEEE/WIC/ACM International Conference on Web Intelligence (WI'05), 666-672.
- Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M., & Monfardini, G. (2008). The graph neural network model. IEEE Transactions on Neural Networks, 20(1), 61-80.
- Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J., & Mei, Q. (2015). Line: Large-scale information network embedding. In Proceedings of the 24th international conference on world wide web, 1067-1077.
- Wang, X., Cui, P., Wang, J., Pei, J., Zhu, W., & Yang, S. (2017). Community preserving network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence, 203-109.