Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信

【ML Tech RPT. 】第13回 機械学習のモデルの評価方法 (Evaluation Metrics) を学ぶ (4)

R&D 連載

f:id:ssatsuki040508:20181210005017p:plain
DSOC研究員の吉村です. 最近, 自室の乾燥が気になってきたので, 湿度計を購入しました. 今までは, なんとなく調子が悪いから乾燥しているな, と思う程度だったのですが, 実際の湿度が具体的に数値で見れるようになったことで, 事前に対策を打てるようになり, QOLが少し上がりました.

さて, 今回も機械学習のモデルの評価方法についてまとめていこうと思います. いよいよ今回からは少し特殊な問題設定における評価指標について見ていきます. 今回は主にマルチラベル分類 (multi-label classification)における精度評価方法について扱います. 一部, ランキング学習 (learning to rank)の評価手法についても述べます.

問題設定が込み入ってくると, それだけ評価の方法は難しくなります. 加えて, それが妥当な評価なのか, 何を測っている指標なのか, という部分も曖昧になってきます. そのため, そういった部分にも注意を向けて今回も見ていきましょう.

マルチラベル分類の精度評価

マルチラベル分類とは, 特定の対象物に対して, 同時に二つ以上のラベルが割り当てられうる, 又は, 同時に二つ以上のクラスに振り分けられうるような問題設定のことを指します. ここで, うる という言葉に下線を引いているのは, 必ずしも全ての対象物に対して二つ以上のラベルが割り当てられるというわけではなく, 一つのラベルしか割り当てられない対象物も存在することを強調するためです. 一方, 特定の対象物に対して, 必ず一つのラベルだけが割り当てられる問題設定をシングルラベル分類と呼びます. 二値分類や多クラス分類がシングルラベル分類にあたります.

本題に入る前に, 先に Notation を整理しておきます.

  • \mathcal{I}: 事例集合.
  • n: 事例の数. n=|\mathcal{I}|.
  • \mathcal{L}: 候補ラベル集合.
  • m: 候補ラベル数. m=|\mathcal{L}|.
  • Y_i \subset \mathcal{L}: 事例 i の真のラベル集合.
  • Z_i \subset \mathcal{L}: 事例 i に対する, 予測ラベル集合.
  • \boldsymbol{y}_i \in \mathbb{R}^m: 事例 i の真のラベルベクトル.
  • \boldsymbol{z}_i \in \mathbb{R}^m: 事例 i に対する, 予測ラベルベクトル.

では, ここからが本題です. マルチラベル分類の評価指標は, 大きく次の 3 つに分けられます.

  • Instance-based Metric
  • Macro-averaged Metric / Label-based Metric
  • Micro-averaged Metric

今回は, これらに加えて, 少し毛色が異なりますがランキング学習でも用いられる評価指標も紹介します.

マルチラベル分類の予測結果は, |\mathcal{I}| \times | \mathcal{L}| 行列の形式で与えられます. (真のラベルの集合も同様の形です.) この時, 下記の図のように行方向 (各事例ごと) に一度評価を行い, それらの平均で合算するのが Instance-based Metric です.

f:id:ssatsuki040508:20191205140338p:plain
Example-based Metric (事例ベースの評価指標) の図.

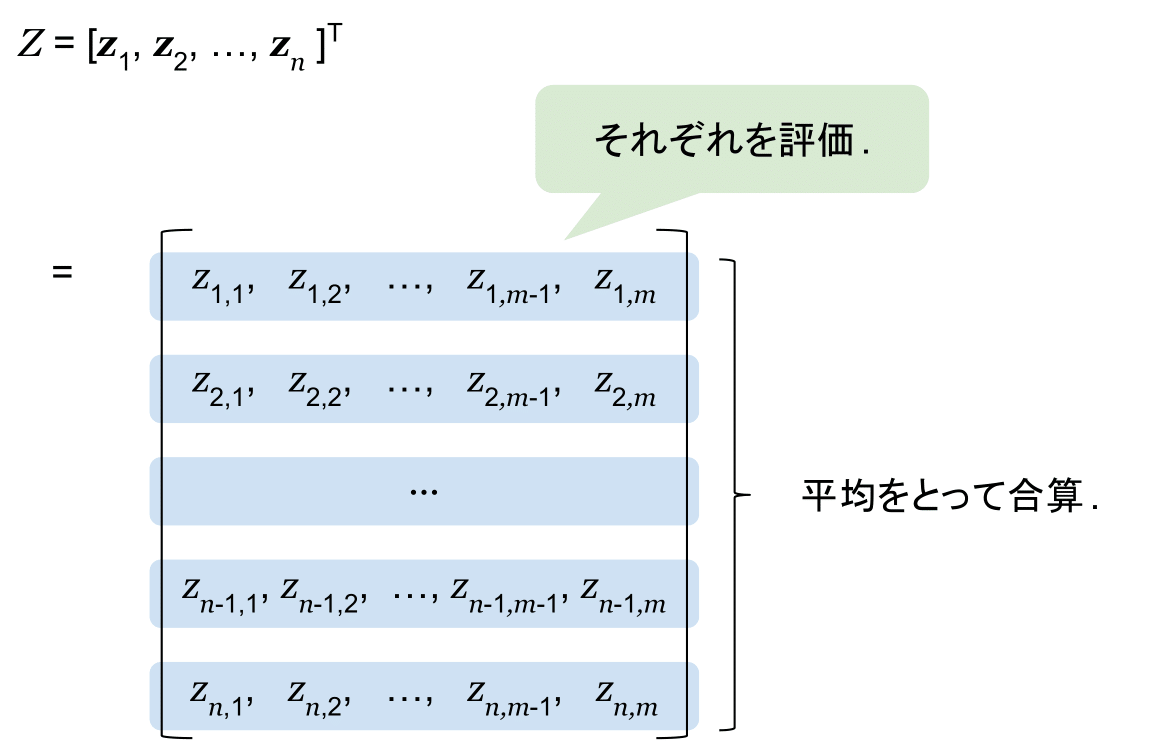
逆に, 下記の図のように列方向 (各ラベルごと) に一度評価を行い, それらの平均で合算するのが, Macro-averaged Metric や Label-based Metric と呼ばれるものです.
f:id:ssatsuki040508:20191205141535p:plain
Macro-averaged Metric / Label-based Metric (ラベルベースの評価指標) の図.

最後に, 全体に対して一括で評価を行うアプローチが Micro-averaged Metric です.

では, これらに所属する具体的な評価指標を見ていきましょう.


事例ベースの評価指標 (Instance-based Metric)

事例ベースの評価指標として, Accuracy[*1], 0/1 Loss, Hamming Loss, Log Loss[*2, *3], Instance-based F_1 score の五つについて紹介します. Instance-based Metric では, 各ラベルに対して全て同じ扱いをします. そのため, Instance-based Metric では, あるラベルに対して適切な予測が一つもできていなかった (True Positive が一つもない) としても, それが明確に現れにくいことに注意が必要です.

Accuracy

二値分類の時も, Accuracy を紹介しましたが, こちらはマルチラベル分類における Accuracy であり, 別のものだと思ってください. これらは, どちらも値が大きいほど性能が良いことを示す指標ですが, 式が異なり, マルチラベル分類の場合には, 下記の式で表されます.
$$\text{Accuracy} = \frac{1}{n}\sum_{i \in \mathcal{I}}\frac{|Y_i \cap Z_i|}{|Y_i \cup Z_i|}$$
二値分類の場合と違ってマルチラベル分類の場合には, 真のラベルの数が事例ごとに異なる点が話をややこしくしています. Accuracy では, この部分を各事例 i ごとに真のラベルの集合 Y_i と予測ラベルの集合 Z_i の和集合の要素数を分母に取ることで対応しています. この指標の良いところは, 各事例 i ごとの評価値を決める際の分母が, たかだか, 真のラベルの集合と予測ラベルの集合の和集合 |Y_i \cup Z_i| の要素数程度である点です.

Hamming Loss

Hamming Loss は, その名前の通りハミング距離で損失を測る指標で, 値が小さいほど性能が良いことを表します.
$$\text{Hamming Loss} = \frac{1}{n}\sum_{i \in \mathcal{I}} \frac{|\boldsymbol{y}_i \bigtriangleup \boldsymbol{z}_i|}{m}$$
ただし, ここで \bigtriangleup は, 二つのベクトルの各要素について XOR 操作をする演算子を意味します. この指標では, 各事例集合ごとに, 真のラベルベクトルの真偽値と, 予測ラベルベクトルの真偽値との間の XOR 演算を取り, 真偽値が異なる部分が全候補ラベル中何個あるかを割合で出して, 全ての事例に対して平均をとっています. Hamming Loss では, Accuracy とは違って, 各事例ごとの評価値は候補ラベル数に依存します. これにより, Accuracy を用いる場合にはそれほど大きく問題にならなかった問題が生じます. 具体的な場合で説明します. 今, 候補ラベル数が 6 個のデータセットがあり, ある事例について, 真のラベル集合が Y=\{l_1, l_2\} として, 予測ラベル集合が Z=\{l_1, l_2, l_6\} だとします. この時, 事例集合数が仮に 1 つしかないとすると, この Hamming Loss の値は, 1/6\approx0.167 となります. 次に, 候補ラベル数が 100 個 のデータセットがあり, ある事例について, 真のラベル集合が Y=\{l_1, l_2\} として, 予測ラベル集合が Z = \{l_3\} だとします. この時, 事例集合数が仮に 1 つしかないとすると, この Hamming Loss の値は, [3/100=0.03] です. Hamming Loss の値は小さいほど良いことを考えると, 値だけを見れば後者の方が, うまくいってそうに感じますし, 前者の方はそれに比べるとうまくいってなさそうに見えます. 当然, 異なるデータセット間の評価を比較すること自体がナンセンスなのですが, ここで言いたいのは出てくる数値が候補ラベル数に依存することによって, 体感と大きく乖離してしまうということです. このような感覚のズレは, Accuracy を用いる場合にはそれほど大きくなりません. 何故ならば, マルチラベル分類においては, 候補ラベル数というのは 容易に十万~百万のオーダになり得ますが, 各事例ごとに割り当てられるラベルの数はどんなに多くても 30 個もつきません. ほとんどの場合はせいぜい 1~5 個程度です (例えば, ここで公開されているデータセット一覧をざっと見ただけでもわかると思います.). したがって, それほど大きく予測を外さない限りにおいて, 各事例ごとに見たときの Accuracy の値の分母が非常に大きくなることはあまりありません.

0/1 Loss

0/1 Loss は, 各事例ごとに真のラベル集合と予測ラベル集合が完全に一致した場合に 0, そうでなければ 1 という評価を下して, 全事例について平均をとった損失です. したがって, この値は小さいほど性能が良いことになります. 実際の式は下記のようになります.
$$\text{0/1 Loss} = \frac{1}{n}\sum_{i \in \mathcal{I}}I[Y_i \neq Z_i]$$
ただし, I[\cdot] は指示関数を表し, 内部の評価式が 真であれば 1, 偽であれば 0 をとります. 0/1 Loss は見ての通り, 事例について全ての真のラベルを過不足なく一致させた時のみ損失が小さくなるため, 様々ある中で一番厳しい評価指標となります. ただ, 部分的に一致していても複数のラベルが完全に一致していなければ意味がないような状況は考えにくいため, 実務の上ではあまり使う場面がない印象です. 基本的に, マルチラベル分類において, どんなに候補ラベル数が多くても, その組み合わせのうち実際に観測されるものはそれほど多くないため, 一度予測した後に学習データ内にあったラベルの組み合わせのうち最も近いものに射影し直すような手法で, 0/1 Loss の性能向上を図ることも可能です. しかし, その場合には訓練データとテストデータの分布がほぼ同じであるような仮定を置く必要があります.

Log Loss

Log Loss は, いわゆる Log Loss をマルチラベル分類に拡張した評価指標で, 下記の二つの式で表されます.
$$\text{Multi-Labeled Log Loss} = \frac{1}{nm} \sum_{i \in \mathcal{I}} \sum_{l in \mathcal{L}} \min{\left(\text{Log-Loss}(\lambda^l_i, y^l_i), \ln{n}\right)}\\
\text{Log-Loss}(\lambda, y)=-\left( y\cdot \ln{(\lambda)} + (1-y)\cdot \ln{(1 - \lambda)}\right)$$
ただし, y_i^l \in \{0, 1\} と \lambda_i^l \in [0, 1] はそれぞれ, 対象物 i に対するラベル l についての真の値と, 予測時の信頼度を表します. この指標では, 信頼度を用いた評価を行なっている点が少し特殊です. これにより, 高い信頼度での誤りに対して多くのペナルティを課し, やや曖昧な信頼度での誤りについては相対的に低いペナルティを課します. また, ペナルティを \ln(n) を用いて制約をかけることで, 非常に少ない部分での非常に大きな誤りによる値の過剰な変化を防いでいます. この指標も, 値が小さいほど性能が良いことを表しており, ベストスコアは 0 です.

Instance-based F_1 score

Instance-based F_1 score は, 下記の二つの式で表されます.
$$ \text{Instance-based } F_1 \text{score} = \frac{1}{n}\sum_{i \in \mathcal{I}} \text{Metric}(\text{TP}_i, \text{TN}_i, \text{FP}_i, \text{FN}_i) \\
\text{Metric}(\text{TP}, \text{TN}, \text{FP}, \text{FN}) = F_1(\text{TP}, \text{TN}, \text{FP}, \text{FN})$$
ここで, F_1 はこちらの記事の中で紹介したもので, 各 \text{TP}_i, \text{TN}_i, \text{FP}_i, \text{FN}_i はそれぞれ, 事例 i に対する, True Positive, True Negative, False Positive, False Negative を表します. この式を説明すると, 事例ごとに F_1 score を計算して, 全事例に対して平均をとっています. この Metric 部分には, Recall, Precision なども利用でき, それぞれ, Instance-based Recall, Instance-based Precision という指標になります.

ラベルベースの評価指標 (Macro-averaged Metric / Label-based Metric)

ラベルベースの評価指標として, Macro-averaged F_1 score を紹介します. ただ, 基本的な枠組みはそのままで, それらを Recall や Precision などに応用できるのでその話も少しだけします. ラベルベースの評価指標では, ラベルの分布に大きな偏りがある場合に, 強い影響を受けやすいという欠点があります. 例えば, あるラベルが全体事例のうち1つしかない場合にそれを外してしまうと, そのラベルについての評価値は最低値になってしまいます. 最終的に, それを含めて平均を取ることを考えれば, それだけで大きなペナルティになることは容易に想像がつきます.

Macro-averaged F_1 score

Macro-averaged F_1 score は, 下記の二つの式で表されます.
$$ \text{Macro-averaged } F_1 \text{score} = \frac{1}{m}\sum_{l \in \mathcal{L}} \text{Metric}(\text{TP}_l, \text{TN}_l, \text{FP}_l, \text{FN}_l) \\
\text{Metric}(\text{TP}, \text{TN}, \text{FP}, \text{FN}) = F_1(\text{TP}, \text{TN}, \text{FP}, \text{FN})$$
ここで, F_1 は, Instance-based F_1 score と同様のもので, 各 \text{TP}_l, \text{TN}_l, \text{FP}_l, \text{FN}_l はそれぞれ, ラベル l に対する, True Positive, True Negative, False Positive, False Negative を表します. この式を説明すると, ラベルごとに F_1 score を計算して, 全ラベルに対して平均をとっています. こちらも, Metric 部分には, Recall, Precision などが利用でき, それぞれ, Macro-averaged Recall, Macro-averaged Precision という指標になります.


ミクロ平均による評価指標 (Micro-averaged Metric)

ミクロ平均による評価指標として, Micro-averaged F_1 score を紹介します. こちらも, 基本的な枠組みはそのままで, それらを Recall や Precision などに応用できるのでその話も少しだけします. ミクロ平均では, 全体をひとまとまりとして評価を行うので, 全てのラベルや事例を区別しないような評価値が得られます.

Micro-averaged F_1 score

Micro-averaged F_1 score は, 下記の二つの式で表されます.
$$\begin{eqnarray}
\text{Micro-based } F_1 \text{score} &=& \text{Metric}(\sum_{l \in \mathcal{L}}\text{TP}_l, \sum_{l \in \mathcal{L}}\text{TN}_l, \sum_{l \in \mathcal{L}}\text{FP}_l, \sum_{l \in \mathcal{L}}\text{FN}_l)\\
&=& \text{Metric}(\sum_{i \in \mathcal{I}}\text{TP}_i, \sum_{i \in \mathcal{I}}\text{TN}_i, \sum_{i \in \mathcal{I}}\text{FP}_i, \sum_{i \in \mathcal{I}}\text{FN}_i)
\end{eqnarray} \\
\text{Metric}(\text{TP}, \text{TN}, \text{FP}, \text{FN}) = F_1(\text{TP}, \text{TN}, \text{FP}, \text{FN})$$
ここで, F_1 は, Instance-based F_1 score と同様のものです. また, 各 \text{TP}_i, \text{TN}_i, \text{FP}_i, \text{FN}_i, \text{TP}_l, \text{TN}_l, \text{FP}_l, \text{FN}_l はいずれも既に定義したもので, この式では, 全体に対する TP, TN, FP, FN の総計を取得して, それを元に F_1 score を計算しています. この Metric 部分には, Recall, Precision なども利用でき, それぞれ, Micro-based Recall, Micro-based Precision という指標になります.


ランキング学習でも用いられる評価指標

ここでは, ランキング学習でもマルチラベル分類問題でも用いられる Precision@ k, Mean Average Precision (MAP, mAP) の二つについて紹介します. ここで紹介する手法の特徴は, 予測結果側はランキングの形式で与えられるのに対して, 正解データは真偽値などの形で与えられている場合に用いる評価指標であることです.

Precision@ k

Precision@ k は, 各事例について信頼度順にラベルを並べたとき, 上位 k 件に対して Precision を計算する指標です. したがって, これは 事例ベースの手法と言え, 最終的には全ての事例に対しての平均を取ることが多いようです. 各事例ごとに適用する評価の式は次のようになります.
$$\text{Precision@}k_i=\frac{\sum_{j=1}^kI[z_{i, S(j)} = y_{i, S(j)}]}{k}$$
ただし, この時 S(j) は, 事例 i の信頼度が上位 j 番目のラベルを表す添字を表します. Precision@ k の k はドメインや, 実際にそのアルゴリズムを使って得られる結果をどのように使うかによって適切に定めると良いです. 例えば, あるユーザに対してより適切な商品を推薦するため, (各ユーザに適切な商品のラベルがつくような) マルチラベル分類を解き, その評価をしたいとします. この時, おそらく重要なのは, せいぜいその推薦画面上で表示する件数でいいはずです. したがって, 仮に 10 個推薦商品を表示するのであれば, k=10 で評価すれば良いだろうと考えられます.

Mean Average Precision (MAP, mAP)

Mean Average Precision は, 全ての事例に対する Average Precision の平均の値です. ある事例 i に対する Average Precision は下記の式で表されます.
$$\text{AP}_i=\sum_{k=1}^n \frac{y_{i, S(k)} \cdot \text{Precision@}k_i}{\sum_{j'=1}^k y_{i, S(j')}}$$
ただし, 場合によっては, 事例 i の真のラベルが全て出た段階までの平均として Average Precision を定義することもあるようで, そちらの方がより自然な定義に思えます.
このような Average Precision の事例ごとの平均をとったものが, Mean Average Precision となります.
$$\text{Mean Average Precision} = \frac{1}{n}\sum_{i\in \mathcal{I}}\text{AP}_i$$
この指標では, より上位だと推定したラベルが当たっているほど, 評価値が高くなります. そういう意味で, 上位の方に予測したラベルが当たっていればそれなりに嬉しい状況で用いる評価指標であると考えられます.

まとめ

今回はマルチラベル分類における評価指標と, それに付随して一部ランキング学習における評価指標を紹介しました. 基本的に, マルチラベル分類では評価に用いる指標にデファクトスタンダードがありません. そのため, 多くの論文では複数の評価指標による評価が行われています. そのことからもわかるように, マルチラベル分類における各種評価は非常に難しいものであるため, 評価したい場合には達成すべき目標から逆算して評価指標を選択, あるいは組み合わせる必要があると思います. 今回も長くなりましたが, 読んでいただきありがとうございます. 次回は, ランキング学習のその他の評価指標などにスポットライトを当ててみようと思います. 今回ご興味を持っていただいた方は, 読者になるボタンをポチッとお願いします.

*1:G. Tsoumakas, I. Katakis, "Multi-Label Classification: An Overview," in IJDWM, 2007

*2:J. Read, B. Pfahringer, G. Holmes, and E. Frank, "Classifier Chains for Multi-Label CLassificaion," in ECML, 2009

*3:J. Read, B. Pfahringer, G. Holmes, and E. Frank, "Classifier Chains for Multi-Label CLassificaion," in ML, 2011

© Sansan, Inc.