f:id:S_aiueo321:20200529093604p:plain

こんにちは，DSOC 研究開発部の内田です．今年の4月に新卒入社いたしました，と言っても以前からインターンしていた関係で連載を持たせてもらっていたので，SBB内では連載のリニューアルの意味合いの方が強いです．コロナ禍により執筆時点で入社後一度も出社できていませんが，連載が1つのモチベーションにでもなればいいなと意気込んでおります．

さて，今回は先日結果が公表されたNTIRE2020 Challengeという超解像のコンペについて書きたいと思います．超解像の中でも，特に実応用に根差した分野にフォーカスしていきます．本エントリでは超解像の基礎的な部分についてあまり触れないので，興味のある方は下記を読んでいただければ恐らく流れは理解いただけるかと思います．

Real-World Image Super-Resolution

2018年以前に主流だった超解像手法の多くは，高解像度(HR)画像からBicubic補間により低解像度(LR)画像を生成してHR-LRペアを生成し，巷で話題のSelf-supervisedな問題として解いていました．その上でGANを用いた学習を導入して知覚的品質を高めようとしていたわけです．しかし，深層学習モデルの社会実装が進む昨今，これらのモデルが実画像に対して上手くいかないことが問題となってきました．

超解像は画像復元問題の一種と考えられ，その過程を見れば、上手くいかない原因は明らかです．

f:id:S_aiueo321:20191106145304p:plain — 画像復元問題としての超解像

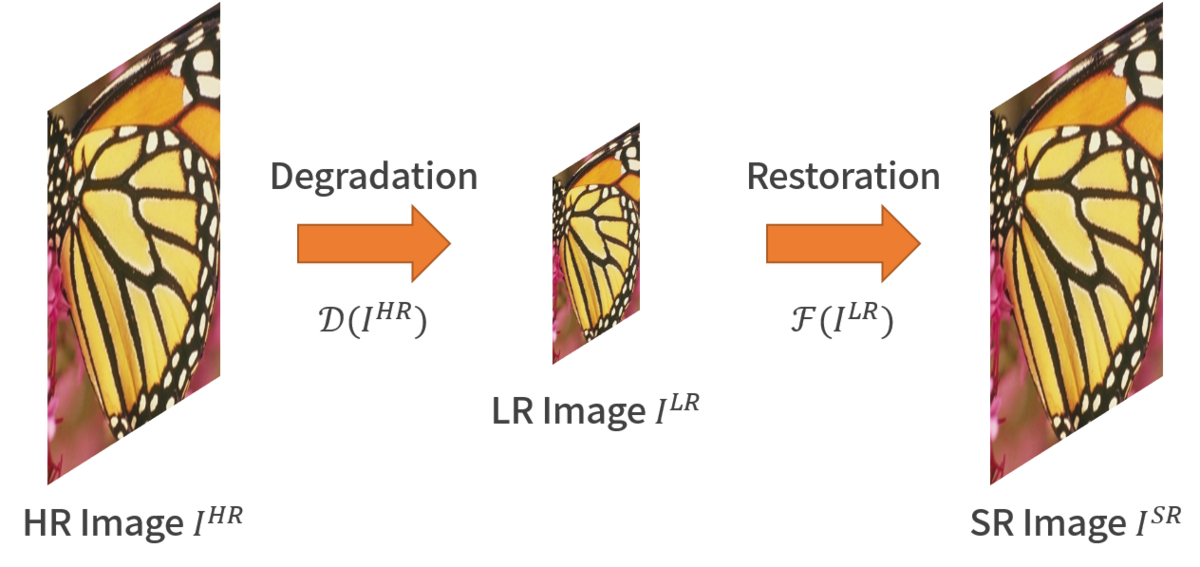
観測されるLR画像は劣化 $\mathcal{D}$ によるHR画像の射影であると仮定すると，画像復元問題を解くことは $\mathcal{D}$ の逆写像 $\mathcal{F}$ を求めることと同値です．実応用を考えた場合， $\mathcal{D}$ は当然未知であり，その程度も一定ではありません．したがって，Bicubic補間のような決め打ちの演算を仮定するのではなく，明示的ないし暗黙的に $\mathcal{D}$ を認識しながら推論する必要がありそうです．

さらに言えば，「iPhoneで撮った画像を大きくしたい」みたいなユースケースではHR画像の入手は困難なので，安易にHR-LRペアから $\mathcal{D}$ を推定することもできません． Real-World Image Super-Resolutionを考える上では，LR画像のみ存在する状況から如何に学習をしていくかが重要となります．

NTIRE2020

概要

NTIRE (New Trends in Image Restoration and Enhancement) は，CVPR併設の画像復元・画像強調分野のワークショップであり，例年コンペティション形式で精度を競い合います。ここで良い成績を残したモデルたちはベースラインとして多く引用されています．今年はトータルで15のトラックが開催され，3つが超解像タスク、うち2つがReal-World Image Super-Resolutionのトラックでした．以下では、各トラックのレギュレーションについて確認していきます．

data.vision.ee.ethz.ch

レギュレーション

ここでは，歪みを含むドメインをソースドメイン $\mathcal{X}$ とし，ノイズを含まないドメインをターゲットドメイン $\mathcal{Y}$ とします．どちらのトラックでも拡大倍率は4倍です．

Track 1: Image Processing Artifacts

問題設定

Track 1では， $\mathcal{X}$ の歪みとしてローエンドの画像処理系で発生する歪みを利用し， $\mathcal{X}$ からサンプリングされたLR画像を， $\mathcal{Y}$ に含まれるようなHR画像に変換するタスクを解きます．ここで $\mathcal{X}$ に付与される歪みは未知であり，歪みのリバースエンジニアリングも禁止です．すなわち， $\mathcal{X}$ の画像を目で見て歪みを予想し， $\mathcal{Y}$ に予想した歪みを付与して学習ペアを作るという行為は禁止されます．ただし，学習を通して劣化をモデリングし， $\mathcal{Y}$ に適用することで学習ペアを作る行為は認められています．

提供されるデータ

ソースドメインの学習データ $\mathcal{X}_{train}^{tr1}$ には，Flickr2K[*1]に対して歪みを付与したものが提供されます．また，ターゲットドメインの学習データ $\mathcal{Y}_{train}$ にはDIV2K[*2]の学習データ800枚をそのまま利用します．ただし， $\mathcal{X}_{train}^{tr1}$ にはダウンサンプルは適用されていないため，Ground Truthは存在せず，生のFlickr2Kを利用しても教師ありの問題としては解けない点に留意してください．

ソースドメインの検証，テストデータ $\mathcal{X}_{val}$ ， $\mathcal{X}_{test}$ には，DIV2Kの該当部分に $\mathcal{X}_{train}^{tr1}$ と同様の歪みを付与して利用します．これらはダウンサンプル後に歪みが付与されるため，生のDIV2Kを $\mathcal{Y}_{val}^{tr1}$ ， $\mathcal{Y}_{test}^{tr1}$ として評価します．

評価方法

評価データにはGround Truthがあり一般的な評価指標が利用可能なため，コンペティション中はPSNR，SSIMを評価指標としたリーダーボードが公開されていました．テストフェーズでは主にLPIPS[*3]で評価し，LPIPSの上位10チームがユーザ評価に進出します．ユーザ評価ではAmazon Mechanical Turkを利用してMOS(Mean Opinion Score)を算出します． MOSは出力画像とGround Truthを比較し，Ground Truthに対して出力画像の品質を6段階('0': Perfect, ..., '5': Terrible)で評価し，その平均を算出した数値です．

Track 2: Smartphone Images

問題設定

Track 2では，実際の低品質なカメラによって撮影された画像に対して超解像を行います．ソースドメインの画像が差し変わるくらいで，問題設定はほぼTrack 1と共通しています．歪みは未知なのが自明ですし，ましてやリバースエンジニアリングなんてできないのであえて禁止されていないというのが相違点と言ったところでしょうか*4．

提供されるデータ

$\mathcal{X}_{train}^{tr2}$ ， $\mathcal{X}_{val}^{tr2}$ には，iPhone3によって収集されたDPED[*5]データセットが提供されます．DPEDデータセットにはGround Truthが存在しないため， $\mathcal{X}_{test}^{tr2}$ は用意せず $\mathcal{X}_{val}^{tr2}$ の一部を利用して最終結果を算出します． $\mathcal{Y}$ に関してはTrack 1と全く同じ設定です．

評価方法

評価データにもGround Truthが存在しないため，一般的な評価指標は利用できません． Ground Truthを必要としない画質評価指標はいくつか提案されていますが，各指標に相関がないため，最終的にはオーガナイザー視点で結果が良かった5チームがユーザ評価に進出します． MOSの算出にはGround Truthが必要となるため，Track 2ではMOR(Mean Opinion Rank)をユーザ評価の結果とします． MORは各手法の出力画像を品質の良い順に並べ替えてもらい，その順位を平均した数値です．

結果

最終順位

f:id:S_aiueo321:20200527004241j:plain

見ての通り，Track 1, 2ともにImpressionismの手法が見事優勝を飾りました 🎉 それぞれのスコアを見ると，他の手法に対して大きな差をつけての優勝だったことが伺えます． AITA-Noahチームは最もImpressionismに近い結果を示していますが，レギュレーション違反が発覚したため，Track 1では残念ながらランク外となっています．

優勝チーム

Impressionismの論文および著者の詳細は下記になります．超解像で強いところは大体CUHKかETHZ絡みみたいな勝手なイメージがあるので，Tencentがこの分野に力入れているのは個人的には意外でした．

タイトル: Real-World Super-Resolution via Kernel Estimation and Noise Injection
著者: Xiaozhong Ji, Yun Cao, Ying Tai, Chengjie Wang, Jilin Li, Feiyue Huang
所属: Tencent Youtu Lab

解法

(注意) 2020/5/26時点でワークショップに投稿された論文は公開されていないため，コンペティションレポートを参考に手法を概説します．余裕があれば，公開後に加筆修正していきます．

多くのチームが昨年のICCVで開催されたAIM2019の解法*6を踏襲する中，Impressionismは明示的なカーネル推定とノイズ注入によって劣化を再現し，ターゲットドメインすら必要としないフレームワークを提案しました．

解法の概要を次の図に示します．

f:id:S_aiueo321:20200526161145p:plain — Impressionismの解法概要

解法は主に4つのステップに分かれており，以下で順に説明していきます．

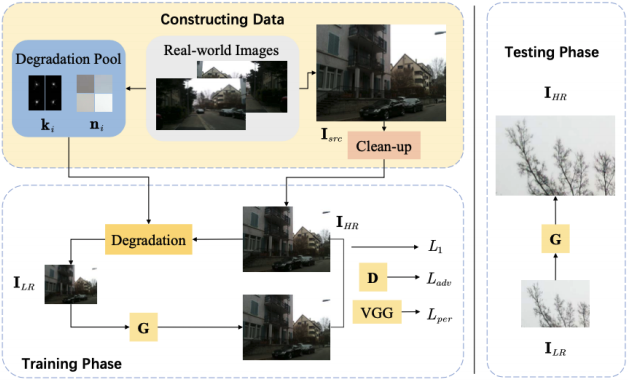
Clean-up

ここでは， $\mathcal{X}$ に対してBicubicダウンサンプリングを適用し，高周波ノイズを除去します．ソースドメインの画像を $\mathbf{I}_\mathrm{src} \in \mathcal{X}$ ，理想Bicubicカーネルを $\mathbf{k}_\mathrm{bic}$ ，倍率を $s$ とすると，Clean-upされた画像 $\mathbf{I}_\mathrm{HR}$ は次式で表されます． ${\displaystyle \mathbf{I}_\mathrm{HR} = (\mathbf{I}_\mathrm{src} \ast \mathbf{k}_\mathrm{bic})\downarrow_s }$ この処理により， $\mathcal{X}$ に含まれるようなノイズは $\mathbf{I}_\mathrm{HR}$ から除かれるので，擬似的に $\mathbf{I}_\mathrm{HR} \in \mathcal{Y}$ とみなせます．

Downsamling

ここでは $\mathcal{X}$ のカーネルを推定し，推定したカーネルを用いてリアルにダウンサンプルされた $\mathbf{I}_\mathrm{D}$ を得ます．ここで $\mathbf{k}_i$ は推定したカーネルであり， $i$ は画像のインデックスです．

${\displaystyle \mathbf{I}_\mathrm{D} = (\mathbf{I}_\mathrm{HR} \ast \mathbf{k}_\mathrm{i})\downarrow_s, i \in \{1, 2, \cdots, m \} }$

カーネルの推定にはKernelGAN[*7]を用います．KernelGANは，下図のように1枚の画像上で Downscale Generator を学習し，その画像が生成されるときに適用されたカーネルを推定する手法です．

f:id:S_aiueo321:20200526175026j:plain — KernelGANの学習

またDownscale Generatorには，ReLUのような非線形な活性化を行わないDeep Linear Networkが用いられるため，学習済みモデルから局所受容野と同じサイズのカーネルを明示的に取得することができます．

f:id:S_aiueo321:20200526224117p:plain — Downscale Generator

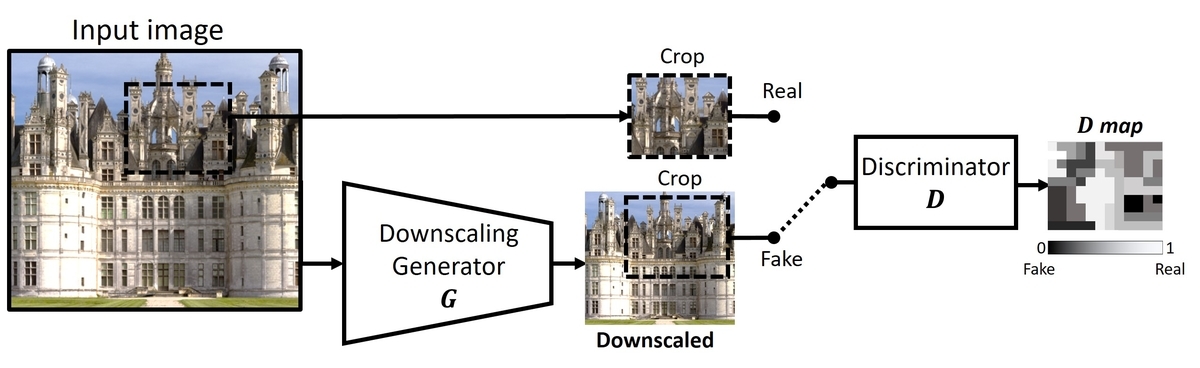
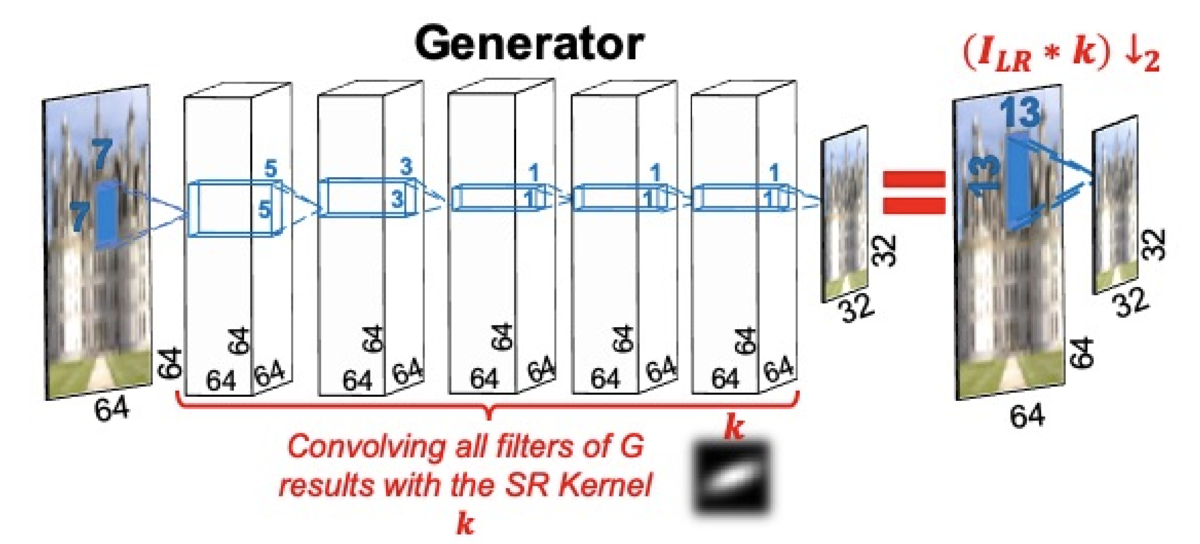
これにより，任意の $\mathbf{I}_\mathrm{src}$ に適用されているダウンサンプルを，学習済みモデルとしてではなく，カーネルとしてプールしておくことができます．プールしたカーネルをランダムに適用することで，効果的なData Augmentationとして振舞うことが期待できます．

Noise injection

実世界の劣化を忠実に再現するには，上述のブラーカーネルによるダウンサンプル以外にも，次式のようにノイズを付与する必要があります．ここで $\mathbf{n}_\mathrm{i}$ はノイズであり，分散が $\sigma^2 (\mathbf{n}_\mathrm{i}) \lt v$ ( $v$ はパラメータ)を満たすようにサンプリングされます．

${\displaystyle \mathbf{I}_\mathrm{LR} = \mathbf{I}_\mathrm{D} + \mathbf{n}_\mathrm{i}, i \in \{1, 2, \cdots, l \} }$

$\mathbf{I}_\mathrm{LR}$ は $\mathbf{I}_\mathrm{HR}$ に対して歪みを付加したものなので， $\mathbf{I}_\mathrm{LR} \in \mathcal{X}$ とみなせます．以上をもって，学習ペア $(\mathbf{I}_\mathrm{LR}, \mathbf{I}_\mathrm{HR}) \in (\mathcal{X}, \mathcal{Y})$ が構築できました．

超解像モデルの学習

上記で構築したペアデータ $(\mathbf{I}_\mathrm{LR}, \mathbf{I}_\mathrm{HR}) \in (\mathcal{X}, \mathcal{Y})$ 上で，ESRGAN[1]ベースのネットワークを学習します*8．誤差関数も一般的なL1 Loss $L_1$ ，Perceptual Loss $L_{per}$ ，Adversarial Loss $L_{adv}$ を組み合わせた形となっています．

${\displaystyle L_{total} = 0.01 \times L_1 + L_{per} + 0.005 \times L_{adv} }$

出力画像の比較

Track 2における出力画像の比較を次に示します*9．各モデルには「Bicubic」が入力されていると考えてもらって差し支えないです．

f:id:S_aiueo321:20200527011143p:plain — 出力画像の比較 (Track 2)

大半の結果は入力画像のノイズをそのまま拡大していたり，独特なパターンが目につきますが，Impressionismの結果はかなりシャープかつ自然な印象です．多種多様なカーネルを明示的に適用できることが，実画像の歪みにも頑健なモデルを構築することに役立っていると予想できます．また，Impressionismは他に比べて色味が入力画像に近く，劣化をCNNなどのブラックボックスでなくカーネルで再現している効果と考えられます．

まとめ

今回はReal-World Image Super-Resolutionにフォーカスし，コンペの問題設定および解法について概説しました．解説した以外の手法を見ていても，ネットワーク構造や誤差関数はほぼ共通していて，いよいよデファクトスタンダードとして確立された感があります．そんな中で各参加者は，どのように学習しやすい問題に落とし込むか，実データと同じ状況を再現するかに注力しており，メタ的に業務に通ずるものを多く感じたので，見習っていきたい気持ちです．

buildersbox.corp-sansan.com

*1:Xintao Wang, Ke Yu, Shixiang Wu, Jinjin Gu, Yihao Liu, Chao Dong, Chen Change Loy, Yu Qiao, and Xiaoou Tang. Esrgan: Enhanced super-resolution generative adversarial networks. ECCV, 2018.

*2:Radu Timofte, Eirikur Agustsson, Luc Van Gool, Ming- Hsuan Yang, Lei Zhang, Bee Lim, Sanghyun Son, Heewon Kim, Seungjun Nah, Kyoung Mu Lee, et al. Ntire 2017 chal- lenge on single image super-resolution: Methods and results. CVPR Workshops, 2017.

*3:RichardZhang,PhillipIsola,AlexeiAEfros,EliShechtman, and Oliver Wang. The unreasonable effectiveness of deep features as a perceptual metric. CVPR, 2018.

*4:だからといってやっていいというわけではないと思いますが…

*5:Andrey Ignatov, Nikolay Kobyshev, Radu Timofte, Kenneth Vanhoey, and Luc Van Gool. Dslr-quality photos on mobile devices with deep convolutional networks. In ICCV, pages 3297–3305. IEEE Computer Society, 2017.

*6:詳しくはこちらを参照いただきたいですが，大まかにいうと事前に劣化モデルを学習してLR-HRペアを作り，その後超解像モデルを学習する手法です．両者の学習時に低周波成分と高周波成分を分けて学習するのが特徴です．

*7:Sefi Bell-Kligler, Assaf Shocher, and Michal Irani. Blind super-resolution kernel estimation using an internal-gan. In NeurIPS, pages 284–293, 2019.

*8:デフォルトのESRGANとの差異は，DiscriminatorとしてPatch Discriminatorを利用しているくらいだそうです．

*9:Track 1の結果はブログに掲載するには差異が細かすぎるので，気になる方は論文の方を参照ください．

Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信

【Zoom or Die】第1回 NTIRE2020 Challenge 結果速報

Real-World Image Super-Resolution

NTIRE2020

概要

レギュレーション

Track 1: Image Processing Artifacts

問題設定

提供されるデータ

評価方法

Track 2: Smartphone Images

問題設定

提供されるデータ

評価方法

結果

最終順位

優勝チーム

解法

Clean-up

Downsamling

Noise injection

超解像モデルの学習

出力画像の比較

まとめ