時間依存性を考慮したWord Embeddingsのまとめ

はじめに

こんにちは、DSOC研究開発部の橋本です。最近買ってよかったな、と思ったものは「詰め替えそのまま」です。これはシャンプーやトリートメントの詰め替えをそのままホルダーにかけて使うことができるようになるグッズで、文字通り（比較的安い）詰め替えをそのまま・簡単に使えるようになる点、お風呂の床に詰め替えを置かなくて済むようになる点という2つの点から非常に良いです。気になる人はぜひググって買ってみてください。
詰め替えそのままの話はさておき、今回時間依存性を考慮したword embeddingsの話をします。

時間に依存するword embeddingsの必要性

現在では、word embeddingsはもはや一般的なツールになりつつあると思います。学習済みのword embeddingsを適用して特徴量とし、何かしらの機械学習アルゴリズムにかける、というのもよく行われていると思います。しかし、過去の学習済みのword embeddingが現在のテキストにもそのまま適用できるか、と言われると、そうでない単語もあると思われます。例えば、コロナ禍以前では「コロナ」という単語は飲料品の文脈などで出ることが多いと思われますが（少なくとも、昔は病気の文脈では数多くは出てこなかったでしょう）、現在は完全にウイルス・疫病の文脈で出現するようになっています。このように、何らかの出来事や時代の変化によって文脈が変わる単語は一定数存在します。したがって、時間依存性を考慮したword embeddingsを得られると、特に最新のテキストを解析する場合には通常の学習済みモデルを使う場合より性能が良くなることがあると考えられます。
word embeddingsの時間依存性を考慮するにあたって、一般的には各時間ごとにword embeddingsを得る方法が主だったようです[1]。しかし、word embeddingsは一般的にnon-convexな学習のため、学習のたびに結果が異なります。そのため、時間ごとのembeddingsの違いを見ようとしたときに、それが本当に時系列推移のシグナルなのか、学習ごとに結果が異なるために生まれるノイズなのか区別がつかない、という問題が発生します。したがって、word embeddingsに時間依存性を導入する際には、モデル・定式化の時点で時間依存性を仮定した上で一括で学習を行うようにすると、より厳密にword embeddingsの時間依存性を捉えられると思われます。
word embeddingsに時間依存性を仮定したモデルはいくつか提案されていますが、今回は主な3つのモデルについて紹介していきたいと思います。

アルゴリズム

Dynamic Word Embeddings (2017)

2017年に発表されたDynamic Word Embeddings [2]では、時間依存するword embeddingsを推定するために2種類の推論方法を提案しています。word embeddingsに時間変化を導入するため、カルマンフィルタ的な取り扱いを行っているのが特徴です。
まずは確率モデルとして、時間に依存するembeddingsを考えてみたいと思います。embeddingsの次元数を $d$ 、総単語数を $L$ 、時間ごとのword embeddingsを $U_{t} = (u_{1, t}, ..., u_{L, t}) \in \mathbb{R} ^{d \times L}$ とし、対応する時間ごとのcontext embeddings を $V_{t}$ と置いて定式化を考えます。
単語とcontext のペアを $(i, j)$ とすると、その $(i, j)$ ペアがコーパスに存在した(しなかった)回数 $n_{ij}^{+} (n_{ij}^{-})$ は上記のembeddingsで以下のようにおけます。

${ \begin{eqnarray} p(n_{t}^{\pm}| U_{t}, V_{t}) = \prod_{i, j=1}^{L} \sigma (u_{i, t}^\top v_{j, t})^{n_{ij, t}^{+}} \sigma (-u_{i, t}^\top v_{j, t})^{n_{ij, t}^{-}} \tag{1} \end{eqnarray} }$

これに、 $U_{t}$ と $V_{t}$ の時間変化を記述する式を置けばよいです。embeddings $U_{t}$ 、 $V_{t}$ の時間推移は

${ \begin{eqnarray} U_{t+1} | U_{t} &\sim& \mathcal{N} \left( \frac{U_{t}}{1 + \frac{\sigma_{t}^{2}}{\sigma_{0}^{2}}}, \frac{1}{ \sigma_{t}^{-2} + \sigma_{0}^{-2}}I \right) \tag{2} \\ V_{t+1} | V_{t} &\sim& \mathcal{N} \left( \frac{V_{t}}{1 + \frac{\sigma_{t}^{2}}{\sigma_{0}^{2}}}, \frac{1}{ \sigma_{t}^{-2} + \sigma_{0}^{-2}}I \right) \tag{3} \end{eqnarray} }$

対応する同時分布は

${ \begin{eqnarray} p(n^{\pm}, U, V) = \prod_{t=0}^{T-1} p(U_{t+1}|U_{t})p(V_{t+1}|V_{t}) \prod_{t=1}^{T} p(n_{t}^{\pm}| U_{t}, V_{t}) \tag{4} \end{eqnarray} }$

となります。
ここで欲しいのは時間に依存するembeddings $U_{t}$ と $V_{t}$ なので、事後分布 $p(U, V | n^{\pm})$ が求めたいものになります。しかし、実際に計算する際に必要になる積分項 $\int p(U, V | n^{\pm}) dUdV$ がintractableなので厳密には求められません。ここでは、Dynamic Skip-Gram Filtering (DSG-F)と、Dynamic Skip−Gram Smoothing (DSG-S)という2つの提案法において、それぞれ近似事後分布を仮定しています。
DSG-Fでは、時間 $t$ におけるembeddingsの近似事後分布を、以下のように仮定します。

${ \begin{eqnarray} q(U_{t}, V_{t}) = \prod_{i=1}^{L} \mathcal{N} (u_{i, t}| \mu_{ui, t}, \Sigma_{ui, t}) \mathcal {N} (v_{i, t}| \mu_{vi, t}, \Sigma_{v i, t}) \tag{5} \end{eqnarray} }$
ここで $\mu$ と $\Sigma$ は最適化したい変分パラメータです。あくまでも時間 $t$ におけるembeddingsの事後分布であるため、時間方向に対して完全に分解されている（独立を仮定している）ことが特徴です。
DSG-Sでは、

${ \begin{eqnarray} q(U_{1:T}) = \prod_{i=1}^{L} \prod_{k=1}^{d} \mathcal{N} (\mu_{ik, 1:T}, \Lambda_{ik}^{-1}) \tag{6} \end{eqnarray} }$
と近似事後分布を仮定します。ここで最適化したい変分パラメータは $\mu_{ik, 1:T}$ と $\Lambda_{ik} \in \mathbb{R}^{T \times T}$ です。 DSG-Sの近似事後分布はDSG-Fとは対照的に、時間方向に対しての依存性を仮定しているのが特徴です。変分パラメータの詳細な更新式や全体のアルゴリズムは元論文[2]を参考にしていただきたいですが、いずれの $\mu$ についても最適化することでそのまま時点 $t$ におけるembeddings （の平均）を得られるため、初期値には学習済みのembeddingsを使用することができます。
DSG-Fでは時間方向は完全に因子分解を仮定していますが、DSG-Sでは時間方向の依存性を仮定しているということもあり、傾向としてはDSG-Sを用いた方がより予測尤度が高いembeddingsの近似事後分布となります。

Dynamic Embeddings for Language Evolution (2018)

Bleiらによって提案された手法であるDynamic Bernoulli Embeddings [3]ではword2vecの分散表現にGaussian Random Walkを仮定します。具体的に言うと、分散表現自体を時間依存する連続潜在変数として扱い、単語がそれに従い生成される、というモデリングを行います。分散表現を連続潜在変数とするモデリング自体は、Exponential Family Embeddings[4]という2016年に提案されたモデルの特殊な場合ではあるのですが、これに時間依存性を組み込んだのがDynamic Bernoulli Embeddingsです。
まずは以前に提案されたExponential Family Embeddingsに倣い、普通のword2vecを確率モデルとして考えてみます。ここではword2vecの中でも、周辺単語集合から該当単語を予測するcontinuous bag of words (以下CBoW)を確率モデル化したいと思います。系列 $x$ における $i$ 番目（ $i = 1, ..., N$ ）の単語 $x_{i}$ （ $L$ 次元のone-hotベクトル）において、 $i$ 番目の単語が $v$ であるかどうかはBernoulli分布で表現することができます。

${ \begin{eqnarray} x_{iv} | \mathbf{x}_{c_{i}} \sim \mathrm{Bern} (p_{iv}) \tag{7} \end{eqnarray} }$

ここで $p_{iv}$ は $i$ 番目の単語が $v$ である確率です。この $p_{iv}$ を直接推定したくなるのですが、推定時に $[0, 1$ ]の制約を無くすため、代わりに対数オッズ $\eta_{iv} = \mathrm{log} \frac{p_{iv}}{1-p_{iv}}$ に変換し、この $\eta_{iv}$ を推定することにします。
実際に推定を行うために、embedding vector $\rho \in \mathbb{R}^{L \times d}$ という $x_{iv}$ 自体の埋め込みと、context vector $\alpha \in \mathbb{R}^{L \times d}$ という周辺の文脈を埋め込むベクトルを定義し、次の形式で書くことにします。

${ \begin{eqnarray} \eta_{iv} = \rho_{v}^\top \left( \sum_{j \in c_{i}} \sum_{v^{'}} \alpha_{v^{'}} x_{jv^{'}} \right) \tag{8} \end{eqnarray} }$

この式では、指定した単語 $v$ 自体の埋め込みと、 $x_{iv}$ の周辺単語の埋め込みベクトルを足し合わせたベクトルの内積をとっており、オッズとして考えても直観的な式かと思います。この $\eta_{iv}$ の形式自体はExponential Family Embeddingsの中で提案されていて、上記の $\rho$ と $\alpha$ を学習することで、確率モデル化したword2vecを学習できる、ということになります。ここまでの内容はExponential Family Embeddingsで提案されたモデルの特別な場合（Bernoulli分布）です。
先程まででCBoWのword2vecを確率モデル化できたので、時間依存性を組み込んだDynamic Bernoulli Embeddingsを説明していきたいと思います。
といっても非常に簡単で、embedding vectorが時間によって異なる ( $\rho$ → $\rho^{(t)}$ )と仮定した上で対数オッズを求め、さらにembedding vectorがGaussian Random Walkする、と仮定すればよいです。

${ \begin{eqnarray} \alpha_{v}, \rho_{v}^{(0)} & \sim & \mathcal{N} (0 , \lambda_{0}^{-1}I) \tag{9} \\ \rho_{v}^{(t)} & \sim & \mathcal{N} (\rho_{v}^{(t-1)} , \lambda^{-1}I) \tag{10} \end{eqnarray} }$
ここで $\lambda_{0}$ 、 $\lambda$ は精度パラメータです。
グラフィカルモデルはこのように書けます。embedding vectorは時間依存、context vectorは時間に依存しないものとし、これらから系列 $x$ が生成されるというイメージです。

f:id:w-hash52:20200724145519p:plain — Dynamic Bernoulli Embeddingsのグラフィカルモデル。[3]のFigure 2より引用。

目的関数ですが、

${ \begin{eqnarray} \mathcal{L} ({ \bf \rho}, {\bf \alpha}) = \mathcal{L}_{\mathrm{pos}} + \mathcal{L}_{\mathrm{neg}} + \mathcal{L}_{\mathrm{prior}} \tag{11} \end{eqnarray} }$

と３つの項からなります。ここで

${ \begin{eqnarray} \mathcal{L}_{\mathrm{pos}} &=& \sum_{i=1}^{N} \sum_{v=1}^{L} x_{iv} \mathrm{log} \sigma (\eta_{iv}) \tag{12} \\ \mathcal{L}_{\mathrm{neg}} &=& \sum_{i=1}^{N} \sum_{v=1}^{L} (1 - x_{iv}) \mathrm{log} (1 - \sigma (\eta_{iv})) \tag{13} \\ \mathcal{L}_{\mathrm{prior}} &=& -\frac{ \lambda_{0}}{2} \sum_{v} \left( \| \alpha_{v} \|^{2}+ \| \rho_{v}^{(0)} \|^{2} \right) \\ &-&\frac{\lambda}{2} \sum_{v, t} \| \rho_{v}^{(t)} - \rho_{v}^{(t-1)} \|^{2} \tag{14} \end{eqnarray} }$

です。 $\mathcal{L}_{\mathrm{pos}}$ はword2vecにおける正例に該当し、 $\mathcal{L}_{\mathrm{neg}}$ は負例に該当します。通常の時間に依存しないword embeddingsを得る際と同様に負例の近似を行いたい場合はNegative Samplingを用いることができます。その場合 $\mathcal{L}_{\mathrm{neg}}$ は

${ \begin{eqnarray} \mathcal{L}_{\mathrm{neg}} &=& \sum_{i=1}^{N} \sum_{v \in \mathcal{S}_{i}} \mathrm{log} (1 - \sigma (\eta_{iv})) \tag{15} \end{eqnarray} }$

と、Negative samples $\mathcal{S_{i}}$ を用いて計算してあげればよいです。
$\mathcal{L}_{\mathrm{prior}}$ の項は正則化の役割を担っています。特に Eq. (14)の第二項が特徴で、一時刻前との差のノルムをとっています。これによって、 $\rho^{(t)}$ が急激に変化し"すぎる"のを防ぐ役割があります。
以上の目的関数を、時間ごとのembedding vector $\rho^{(t)}$ と context vector $\alpha$ をパラメータとして最適化させることで、時間依存したembeddingsを得られます（元論文ではAdagradを用いていました）。
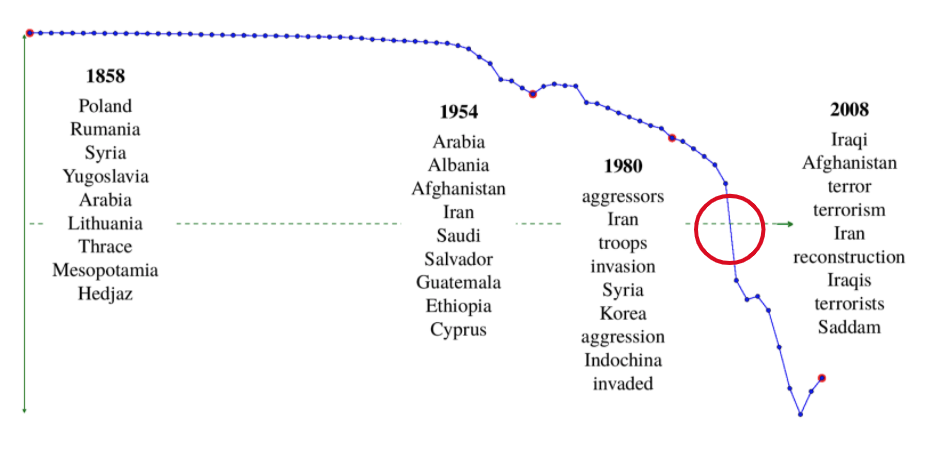
簡単に結果を示したいと思います。アメリカ上院議会のスピーチにおいて"IRAQ" という言葉の文脈変化を示したのが下の図です。横軸が時間、縦軸が $\rho^{(t)}$ の第一主成分なのですが、赤丸の部分（1990-1992）年に最も急峻な変化を示していることがわかります。実際に1990年には湾岸戦争が勃発しており、納得感のある結果かと思います。また、1858年、1954年、1980年、2008年における"IRAQ"の周辺に特に出現した単語も示されていますが、実際に戦争に関連する語が現れており、社会の状態を反映していると言えます。

f:id:w-hash52:20200727173119p:plain — "IRAQ"のembedding vectorの時間変化。[3]のFigure3より引用。赤丸はブログ筆者が追加。

Dynamic Word Embeddings for Evolving Semantic Discovery (2018)

この論文で提案された手法[5]では、時間ごとに正の相互情報量 (Positive Pointwise Mutual Information, PPMI) 行列を設計し、それを行列分解するアプローチによって各時間ごとのembeddingsを求めています。PPMIは次の式で定義されます。

${ \begin{eqnarray} PPMI (x, y) = \mathrm{max} \left(0, \mathrm{log} \frac{P(x, y)}{P(x)P(y)} \right)\tag{16} \end{eqnarray} }$

$P(x)$ 、 $P(y)$ はそれぞれ $x$ 、 $y$ の生起確率、 $P(x, y)$ は $x$ と $y$ が同時に生起する確率を表しています。つまり、独立を仮定した場合と比較してどれだけ共起する確率が高いか・どれだけ関連性が高いかを示す尺度になります。 $\mathrm{max}$ をとっているのは、共起する回数が0の場合 $\mathrm{log} 0 = - \infty$ となるのを防ぐためです。
時間 $t$ におけるPPMI行列を $Y_{t}$ 、時間ごとのembeddingを $U_{t}$ とおくと、最適化したい目的関数は以下のように設計できます。

${ \begin{eqnarray} L (U_{1}, ..., U_{t}, ..., U_{T} )= \frac{1}{2} \sum_{t=1}^{T} \| Y_{t} - U_{t}U_{t}^{\top} \|^{2} \\ \\ + \frac{ \lambda }{2} \sum_{t=1}^{T} \| U_{t} \| ^2 + \frac{ \tau }{2} \sum_{t=1}^{T} \| U_{t-1} - U_{t} \| ^2 \tag{17} \end{eqnarray} }$

ここで、 $\lambda$ 、 $\tau$ は正則化パラメータです。第1項はPPMI行列の復元、第2項はembeddingsの正則化、第3項は[4]の目的関数と同様に $U_{t}$ の急激な変化を抑えるための項となります。
以上の目的関数を $U_{1}, ..., U_{t}, ..., U_{T}$ で最適化すれば、各時間ごとのembeddings $U_{t}$ を求めることができます。
こちらの論文も、簡単に結果の一部を示したいと思います。以下のテーブルは、あるクエリに対し当時のどのような単語に近いかというものを示しています。これを見ると、例えばtwitterは昔のblogやchatに近いということを意味しており、納得感のある結果かと思います。

f:id:w-hash52:20200727172507p:plain — クエリに対する当時の近い単語。[5]のTable 1より引用。

まとめ

今回は、時間に依存したWord Embeddingsのアプローチについていくつか論文を交えて紹介しました。どの論文でも、時間ごとに学習すると学習由来のノイズと時系列推移の区別がつかない・より厳密にword embeddingsの時間依存性を捉えたいというところに課題感を抱えた上で提案された、という部分は同じでしたが、そこからの定式化・アプローチはそれぞれ全く異なっていたのが非常に興味深かったです。
これらの手法の定量的な評価においては、[2]・[3]では予測尤度、[5]ではNMI (Normalized Mutual Information) などの指標において、時間に依存しない通常のword embeddingsを上回っていました。一方で、定性評価についてはいくらか図で示しましたが各論文でかなり多様性があり、[2]においては他の単語との類似度の時間変化、[3]では指定した単語周辺の文脈の時間変化やその時間変化が大きかった時点、[5]では指定した単語が昔のどのような単語に該当するか（あるいは近いか）などを調べていました（個人的には、論文[3]は定式化もシンプルで定性評価も結果がはっきりしており、素晴らしいなと思いました）。
今回紹介した方法で得られるembeddingsに対してこれらの定性的な評価方法を相互に適用してみると、それぞれのembeddingsの得意なことや苦手なことが分かり面白いのではないかと思います。

参考文献

[1] Vivek Kulkarni, Rami Al-Rfou, Bryan Perozzi, and Steven Skiena, "Statistically Significant Detection of Linguistic Change", in WWW, 2015.
[1411.3315] Statistically Significant Detection of Linguistic Change

[2] Robert Bamler, Stephan Mandt, "Dynamic Word Embeddings", in ICML, 2017.
[1702.08359] Dynamic Word Embeddings

[3] Maja Rudolph, David Blei, "Dynamic Embeddings for Language Evolution", in WWW, 2018.
https://dl.acm.org/doi/10.1145/3178876.3185999

[4] Maja R. Rudolph, Francisco J. R. Ruiz, Stephan Mandt, David M. Blei, "Exponential Family Embeddings", in NIPS, 2016.
[1608.00778] Exponential Family Embeddings

[5] Zijun Yao, Yifan Sun, Weicong Ding, Nikhil Rao, Hui Xiong, "Dynamic Word Embeddings for Evolving Semantic Discovery", in WSDM, 2018.
[1703.00607] Dynamic Word Embeddings for Evolving Semantic Discovery

buildersbox.corp-sansan.com
buildersbox.corp-sansan.com