Sansan Tech Blog

Sansanのものづくりを支えるメンバーの技術やデザイン、プロダクトマネジメントの情報を発信

ベイジアン操作変数法でA/Bテストをしよう

R&D 計量経済学 社会科学 新卒

こんにちは。4月に24新卒として入社しました、技術本部 研究開発部の金髙です。大学院では政治学の研究をしていました。

本記事では、筆者が2024年2月から約1カ月間の内定者インターン時代に取り組んだ内容の一部である「ベイジアン操作変数法を用いたA/Bテスト」について紹介します。

背景

筆者が現在所属している研究開発部のチームでは、データドリブンな意思決定やデータ活用促進を目標に掲げています。その一環として、A/Bテストを積極的に行っており、筆者は中でも「Sansanモバイルアプリ内訴求」に関するA/Bテストのタスクに取り組みました。中身としては、ある機能に関するアプリ内訴求はユーザーの当該機能利用につながるのか？を検証したものになります。以下のような訴求メッセージの配信有無をテスト対象ユーザーにランダムに割り当てることで、訴求効果を検証しました*1。

アプリ内訴求メッセージの例

その中でもA/Bテストにベイジアン操作変数法を導入した事例について説明します。これは以下で説明するように、処置に問題がある場合やベイズ統計の枠組みでA/Bテスト検証を行いたいケースで特に有効な手法になります。

関連して、チームメンバーが先月末に『A/Bテストを推進しようとしている話』というテックブログ記事を公開しました。Sansan社内でデータに基づく意思決定を浸透させるべく、A/Bテストの活用推進への挑戦について詳しく書かれています。興味のある方は併せてご覧ください。

buildersbox.corp-sansan.com

なぜA/Bテストで操作変数法なのか？

一般的なA/Bテストのフレームワークでは、テスト対象となるユーザーを抽出し、訴求の有無をランダムに割り振ります。その後、処置を受けた（=訴求あり）グループと受けてない（=訴求なし）グループについてt検定や最小二乗法（Ordinary Least Squares; OLS）などを用いて利用率の統計的に有意な差を検証します。もし有意な差が観測されれば、訴求施策が効果的であると判断されます。

しかし、筆者が実施したA/Bテストでは、訴求ありグループに割り当てられたとしても訴求を閲覧しないユーザーがいるという状況でした。これにより、通常の統計手法を使用すると、訴求の効果が実際よりも低く見積もられる問題が発生しました。

この点について、「それなら訴求を閲覧した人とそうでない人を比べちゃおうよ！」という考えもあるかもしれません。悲しいことに、訴求閲覧という行為の背後には「もともと利用意欲が高いから訴求閲覧もするのでは」というある種のセレクションの可能性が潜んでいるため、一筋縄では検証がうまくいきません。

そこで、上記の問題に対処するために、操作変数法（Instrumental Variable; IV）を用いることにしました。計量経済学でのオーソドックスなIVは、観察データ分析で欠落変数バイアスや逆因果などの問題に上手く対処する際に利用されます。A/Bテストのようなランダム比較化試験（Randomized Controlled Trial; RCT）において、IVはEncouragement designとして利用されています。ランダムな割り当てをしたのにも関わらず、実際には処置を受けていないといった、被験者の処置への非遵守（non-compliance）が起こってしまう状況に対応するために、IVによる効果検証が行われます。

今回のテストケースも同様にして非遵守が発生しており、アプリ機能の利用を促す訴求配信の効果を見にいきたいが、実際に処置群にアサインされても訴求を閲覧しないユーザーが存在します。このような状況において実験グループ間での差を求めてしまうと、実際の処置による効果ではなく、処置意図（Intention-to-Treat; ITT）が推定されることになります。

そこで、実際に処置を受けたかという変数に対して、処置のランダム割り当て（=encouragement）を操作変数として用いることで、処置割り当てに遵守したユニットに対する局所的平均因果効果（Local Average Treatment Effect; LATE）を推定することができます。

Encouragement design

処置非遵守に対処するためのEncouragement designとしての操作変数法（Angrist, Imbens & Rubin, 1996）について簡単に見ていきます。

テスト対象ユーザーが n人いるとし、ある個人を iとして表記します。また、Rubinの潜在アウトカムフレームワークを用いて以下を導入します:

  • Z_i \in \{0, 1\}: ランダムな処置割り当て（操作変数）
  • D_i(z) \in \{0, 1\}: 潜在的な処置ステータス
  • Y_i(d, z),\ \ Y_i(z): 潜在的なアウトカム

訴求配信の例で言えば、 Z_iは訴求配信の有無、 D_iは訴求閲覧の有無、 Y_iは機能利用となります。

ここで、ユーザーの処置割り当てと実際の処置ステータスの関係を見てみると、以下の4つの属性が出てきます:

  • Complier: 処置割り当てを遵守する ( D_i(1) = 1 and D_i(0) = 0)
  • Always-taker: 処置割り当てに関係なく、常に処置を受け取る ( D_i(1) = D_i(0) = 1)
  • Never-taker: 処置割り当てに関係なく、常に処置を受け取らない ( D_i(1) = D_i(0) = 0)
  • Defiers: 処置割り当てに対して真逆を取る ( D_i(1) = 0 and D_i(0) = 1)

各属性を表にまとめると以下のようになります:

Z_i=1 Z_i=0
D_i=1 Complier / Always-taker Defier / Always-taker
D_i=0 Defier / Never-taker Complier / Never-taker

まずは、遵守状況を無視した場合に得られる処置意図（ITT）を見てみましょう。ITTは処置割り当て自体の平均因果効果となるので、以下で表せます:


\begin{align*}
\text{ITT} &= \mathbb{E}[Y_i(1) - Y_i(0)]
\end{align*}

属性ごとのITTを考えることによって、以下のようにITTを分解できます:


\begin{align*}

\text{ITT}
&=\text{ITT}_c\times \Pr(\text{complier})\ +\ \text{ITT}_{a}\times \Pr(\text{always-taker})\\ 
&+\ 
\text{ITT}_{n}\times \Pr(\text{never-taker})\ +\ 
\text{ITT}_d\times \Pr(\text{defier})

\end{align*}

ここで、属性ごとのITTは:


\begin{align*}
\text{ITT}_c &= \mathbb{E}[Y_i(D_i(1), 1) - Y_i(D_i(0), 0)\mid D_i(1) = 1, D_i(0) = 0],\\
\text{ITT}_{a} &= \mathbb{E}[Y_i(D_i(1), 1) - Y_i(D_i(0), 0)\mid D_i(1) = D_i(0) = 1],\\
\text{ITT}_{n} &= \mathbb{E}[Y_i(D_i(1), 1) - Y_i(D_i(0), 0)\mid D_i(1) = D_i(0) = 0],\\
\text{ITT}_d &= \mathbb{E}[Y_i(D_i(1), 1) - Y_i(D_i(0), 0)\mid D_i(1) = 0, D_i(0) = 1].
\end{align*}

\text{ITT}_cは処置遵守者に対する平均因果効果を現しており、私たちが求めようとしているLATE ( \tau_{\text{LATE}})を指します。単純にITTを求めた場合、私たち分析者が本当に欲しい \text{ITT}_c =\tau_{\text{LATE}}以外も含まれてしまうことになります。

それでは、どのようにして \text{ITT}_cを求めれば良いのでしょうか？以下の3つの仮定を天下り的に導入します:

  • Assumptions
    1. Monotonicity (単調性): D_i(1) \geq D_i(0)
      • 割り当ての真逆が起きない（Defierが存在しない）。
    2. Exclusion Restriction (除外制約): Y_i(d, 1) - Y_i(d, 0) = 0
      • 割り当ては実際の処置ステータスを通してのみアウトカムに影響を与える（Always, Never-takerに対するITTが0である）。
    3. Relevance (関連性): \mathbb{E}[D_i(1) - D_i(0) ] \neq 0
      • 実際の処置ステータスに対する割り当て効果が0ではない。

上記3つの仮定が満たされるならば、 \tau_{\text{LATE}} = \text{ITT}_cを求められます*2:


\begin{align*}

\text{ITT} =&\ \text{ITT}_c\times \Pr(\text{complier})\ +\ \text{ITT}_{a}\times \Pr(\text{always-taker})\\ 
&+\ 
 \text{ITT}_{n}\times \Pr(\text{never-taker})\ +\ 
0 \ \ \ (\because \text{monotonicity})\\
=\ &\text{ITT}_c\times \Pr(\text{complier})\ +\ 0\times \Pr(\text{always-taker})\\ 
&+\ 
0\times \Pr(\text{never-taker})\ +\ 
0 \ \ \ (\because \text{Exclusion Restriction})\\
= \ &\text{ITT}_c\times \Pr(\text{complier})

\end{align*}

となり、


\begin{align*}
\text{ITT}_c &= \frac{\text{ITT}}{\Pr(\text{complier})}\\
&= \frac
{\mathbb{E}[Y_i\mid Z_i = 1] - \mathbb{E}[Y_i \mid Z_i = 0]}
{\mathbb{E}[D_i\mid Z_i = 1] - \mathbb{E}[D_i \mid Z_i = 0]}\\
&= \frac{\text{Cov}(Y_i, Z_i)}{\text{Cov}(D_i, Z_i)}
\end{align*}

として求められるようになりました*3。Relevanceが満たされなければ {\text{Cov}(D_i, Z_i)}が0となってしまうことに留意してください。また、上式の標本対応 \widehat{\text{Cov}}(Y_i, Z_i)/\widehat{\text{Cov}}(D_i, Z_i)はWald推定量と呼ばれ、従来のIV推定量や二段階最小二乗推定量と一致します。

非遵守が起こる状況において、上述の3つの仮定が満たされるならば、遵守者に対する平均因果効果である \tau_{\text{LATE}}を求められます。

One-sided Noncompliance

今回行ったA/Bテストでは、訴求あり群に割り当てられたユーザーのみが訴求を閲覧できるような設定となっています。そのため、単調性が保証されるので、defierを除外でき、また D_i(0)=1とはならないことからalways-takerも除外できます。よって、考えるべきユーザー属性がcomplierとnever-takerとなるので、後々の推論が楽になるというメリットを享受できます。このようなコントロール群ユーザーが実際の処置にアクセスできない状況のことをOne-sided Noncompliance（片側非遵守）と呼びます。

訴求が出された ( Z_i = 1) 訴求が出されてない ( Z_i = 0)
訴求を見た ( D_i = 1) Complier / Always-taker Defier / Always-taker
訴求を見てない ( D_i = 0) Defier / Never-taker Complier / Never-taker

さらに嬉しいことに、すべてのユーザー iについて D_i(0) = 0となる（訴求なしユーザーが訴求閲覧することはない）ため、 \boldsymbol{\tau_{\text{LATE}}}と処置を受けたユーザーにおける平均因果効果（Average treatment effect on the treated; ATT）が等しくなります:


\begin{align*}
\tau_{\text{LATE}} &= \mathbb{E}[Y_{i}(1) - Y_{i}(0) \mid D_i(1) = 1, D_{i}(0) = 0]\\
&= \mathbb{E}[Y_{i}(1) - Y_{i}(0) \mid D_i(1) = 1]\ \ \ \because\ \  D_{i}(0) = 0 \ \ \forall\ \ i\\
&= \tau_{\text{ATT}}
\end{align*}

LATEは遵守者における平均因果効果という若干解釈がトリッキーなものでしたが、ATTだと実際に処置を受けた（i.e., 訴求を見た）ユーザーに対する平均因果効果であるので解釈が比較的しやすく、分析者にとっては非常に嬉しいご利益があります。

なぜA/Bテストでベイズなのか？

前セクションまでは、RCTやA/Bテスト環境において、なぜ・どのようにして操作変数法を用いるのかについて概観しました。ここで、タイトルをよく見てみると「ベイジアン」の文字列があることがわかりますね。そう、ベイズ推論の枠組みでA/Bテストを行います。しかし、なぜベイズなのか？以下で頻度論的な従来のA/Bテストの限界点とベイズ推論の利点を見てみます。

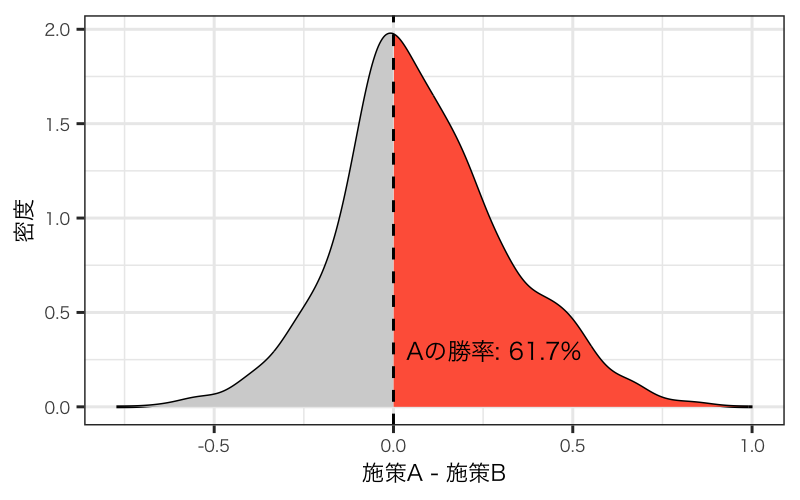
前述の通り、頻度論的なA/Bテストでは実験グループ間の反応差によって処置の有効性を見に行くことが多いです。従来の統計的な基準で言えば、p値が0.05を下回った、いわゆる統計的に有意な差が見られる場合です。しかし、このような従来の統計的有意差に頼った効果検証には限界があります。仮にある介入施策のp値が0.11だとして、帰無仮説が棄却されないとしても、効果がないことを意味しません。さらに言えば、頻度論的な推論で得られる信頼区間の解釈は非常にトリッキーであり、意思決定が必要な場面において適切に扱うのは困難を伴います。施策Aが施策Bと比べてどの程度優れているのか、どの程度有効性があるのかについて、直観的な判断を下せないというのが従来の頻度論的A/Bテストの限界点でもあります。

そこで嬉しいのがベイジアンA/Bテストです。この枠組みでは、グループごとの利用率などを確率変数として扱い、それぞれの事後分布を求めることになります。そのため、最終的に得られるものが確率分布のため、テストグループごとの利用率に関するパラメータの確率的な比較が可能となります。例えば「Aという施策はBという施策に対して優れている確率がXX%くらいある」や「訴求の介入効果が0以上である確率はYY%」であるというような直感的かつ定量的な判断を容易にできるようになります。

ベイジアンA/Bテストである施策AのBに対する勝率を求めた例

ベイジアン操作変数法

操作変数法とベイジアンA/Bテストの嬉しいところを引き継いだのが、ベイジアン操作変数法を用いたA/Bテストです。中身について、今回のA/Bテストケースと照らし合わせながら見ていきましょう。モデルの組み立てに関して、Imbens&Rubin（1997, 2015）によるBayesian Model-based IVを参考にして行っているので、より詳しい内容を知りたい方はそちらをご参照ください。

ここでは今回のA/Bテスト事例と同様のOne-sided Noncomplianceなケースにおけるベイジアン操作変数法について見ていきます。また、データ設定についても今回のA/Bテストケースと同様のものを利用します*4:

  • Y: 機能利用したかどうか（二値）
  • D: 実際に訴求を閲覧したかどうか（二値）
  • Z: 処置割り当て（操作変数, 二値）

簡単化のために以下を導入します:

  • \{ct, cc, nt\}: ユーザー属性
    • ct: 処置群かつ遵守
    • cc: コントロール群かつ遵守
    • nt: Never-taker
  • C_i: 遵守者かどうかを表す変数; 遵守者であれば1,そうでなければ0
  • \mathcal{S}_{ct}: 処置群の遵守者の集合
  • \mathcal{S}_{cc}: コントロール群の遵守者の集合
  • \mathcal{S}_{nt}: Never-takerの集合

データ生成過程

各ユーザー属性ごとの機能利用率に関するパラメータ:

  • \boldsymbol{\theta} = \{\theta_{ct}, \theta_{cc}, \theta_{nt}\}
    • \theta_{ct}: 処置群における遵守者の機能利用率
    • \theta_{cc}: コントロール群における遵守者の機能利用率
    • \theta_{nt}: Never-takerの機能利用率

今回のA/Bテスト事例ではアウトカムは機能利用でしたので、 Y_iは利用したか否かを表す二値変数とし、ベルヌーイ分布から生成されるとします:


\begin{align*}
Y_{i\in\mathcal{S}_{g}} &\sim Bernoulli(\theta_{g})\ \ \ \text{for}\ \ \ g = ct, cc, nt.
\end{align*}

\boldsymbol{\theta}について、以下のような事前分布を定めておきます:


\begin{align*}
\theta_{g} &\sim Beta(\alpha_0^g,\; \beta_{0}^g)\; \; \; \text{for}\; \; \; g = ct, cc, nt.
\end{align*}

事後分布

事後分布は以下のように表せます:


\begin{align*}
p(\boldsymbol{\theta} \mid Y) &\propto p(\boldsymbol{\theta})p(Y\mid \boldsymbol{\theta})\\
&\propto
\theta_{ct}^{\alpha_0^{ct}-1}(1-\theta_{ct})^{\beta_0^{ct}-1}\\

&\times\theta_{cc}^{\alpha_0^{cc}-1}(1-\theta_{cc})^{\beta_0^{cc}-1}\\

&\times \theta_{nt}^{\alpha_0^{nt}-1}(1-\theta_{nt})^{\beta_0^{nt}-1}\\

&\times \prod_{i\in \mathcal{S}_{ct}} \theta_{ct}^{Y_i}(1 - \theta_{ct})^{1 - Y_i}\\

&\times \prod_{i\in\mathcal{S}_{cc}}\theta_{cc}^{Y_i}(1 - \theta_{cc})^{1 - Y_i}\\

&\times \prod_{i\in\mathcal{S}_{nt}}\theta_{nt}^{Y_i}(1 - \theta_{nt})^{1 - Y_i}
\end{align*}

早速 \boldsymbol{\theta}の事後分布を導出したいところですが、コントロール群にいるユーザーがcomplierなのかnever-takerなのかがわからなければ（処置群ユーザーの C_iはわかってる） \theta_{cc}, \theta_{nt}の事後分布を求められません。実際に生データを直接みて「あ、この人はcomplierだな」と断定するのはまぁ困難です。

そこで、コントロール群ユーザーの属性を欠測値として扱い、それをimputeするような戦略を取ることでこの問題に対処します。一見トリッキーですが、有限混合モデルを推定する際のような状況を考えてみれば非常に単純です。そこでは、ある観測個体がどのクラスターに属するかに関する情報を欠測値として扱い、ベイズ更新を用いてデータからクラスターの所属確率を更新するかと思います。それと同じく、コントロール群のユーザーに対してベイズルールを用いることでcomplier確率を求めてやれば良いと考えられます。

ここで、ベイズ更新を行うために、あるユーザー iがcomplierである確率 \Pr(C_i = 1)を \piと置きます。言い換えれば、テスト対象ユーザーに占める \mathcal{S}_{ct}のユーザーを含めたcomplierの割合を表します。この時、コントロール群のユーザーがcomplierである確率 \zeta_iは以下のようにして求めます:


\begin{equation}
\zeta_i = \frac
{
\pi \cdot p(Y_{i}\mid \theta_{cc})
}

{
\pi \cdot p(Y_{i}\mid \theta_{cc}) + 
(1-\pi) \cdot  p(Y_{i}\mid \theta_{nt})
}\ \ \ \text{for}\ \ \ i \in \text{Control group}
\end{equation}

また、今回はベイズ推定の枠組みに則って行うので、その更新された確率からあるユーザーがcomplierかどうかを表す二値変数をベルヌーイ分布からドローすることにします:


\begin{equation}
C_i \sim Bernoulli(\zeta_i) \ \ \ \text{for}\ \ \ i \in \text{Control group}\end{equation}

これで、すべてのユーザーに対する C_iがわかるようになったため、 \mathcal{S}_{cc}, \mathcal{S}_{nt}を特定できます。

追加で、先ほど遵守者割合の新たなパラメータ \piを導入したため、それについても事後分布を求めてやる必要があります。Complierかどうかを表す変数である C_iがベルヌーイ分布に従うため、事前分布をベータ分布として置ければ事後分布もベータ分布となります。事前分布を以下とすれば:


\pi \sim Beta(d_0,\; e_0),

事後分布は、


\begin{equation}
\pi^{post} \sim Beta\left(
d_0 + \sum_{i=1}^nC_i, \ \ 
e_0 + n - \sum_{i=1}^nC_i
\right)
\end{equation}

となります。

残りの \boldsymbol{\theta}に関しても事後分布を導出しましょう。事前分布がベータ分布なので、遵守者割合の事後分布と同様にすれば以下のような事後分布が求まります:


\begin{align}
\theta_{g}^{post} &\sim Beta\left(\alpha_0^{g} + \sum_{i\in\mathcal{S}_{g}}Y_{i},\ \ \beta_0^{g} + |\mathcal{S}_{g}| - \sum_{i\in\mathcal{S}_{g}}Y_{i}\right)\ \ \ \text{for}\ \ \ g = ct, cc, nt.
\end{align}

ここで、 |\cdot|は集合 \cdotの長さを表します。 |\mathcal{S}_{ct}|であれば、処置群で実際に訴求を閲覧したユーザー数となります。

LATEの事後分布推定

Imbens&Rubin（2015）で紹介されている方法に倣ってLATEを推定する場合、以下のようになります:


\begin{equation}
\hat\tau_{\text{LATE}} = \frac{1}{\sum_{i=1}^nC_{i}} \sum_{i:C_i=1} \{Y_i(1) - Y_i(0)\}.
\end{equation}

手順としては

  1. コントロール群のユーザーがcomplierかどうかをパラメータの事後分布を用いて判別
  2. Complierについて、潜在アウトカム Y_i(1 - D_i, 1 - Z_i)を \theta_{ct}, \theta_{cc}から生成する
  3. Complierについてのアウトカムの差の平均を計算する

で、LATEを求められます。

シミュレーションしてみる

実際にシミュレーションを通して、どのようにしてベイジアン操作変数法を行うかをみていきましょう。今回は Python でデータ生成から推定まで行います。

悲しいことに、コードをベタ貼りしてしまうと非常に長くなってしまうので、以下に埋め込んだ Notebook を参考にシミュレーションを体験してみてください。

下図はシミュレーション結果であり、パラメータの事後分布が描画されています。また、各パネルの破線はパラメータの真値を表します。

各パラメータの事後分布（破線は真値を表す）

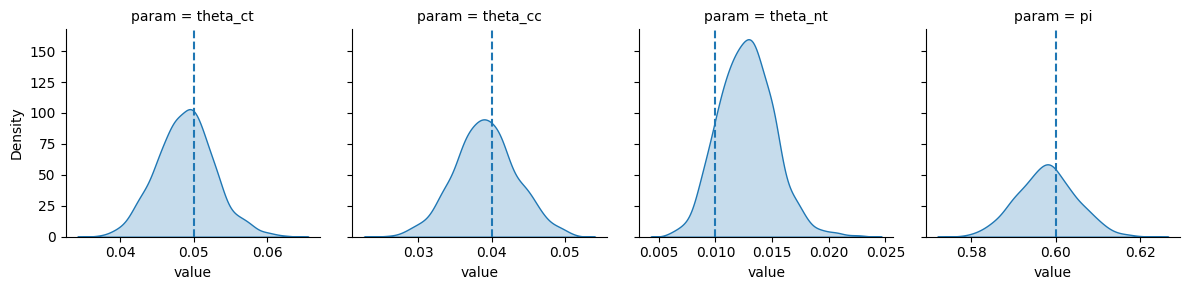
パラメータの事後分布推定は大体うまくいってそうです。パラメータの事後分布を用いて LATEの事後分布推定 の箇所を参考にすれば、簡単にLATEを求められます。

LATEの事後分布

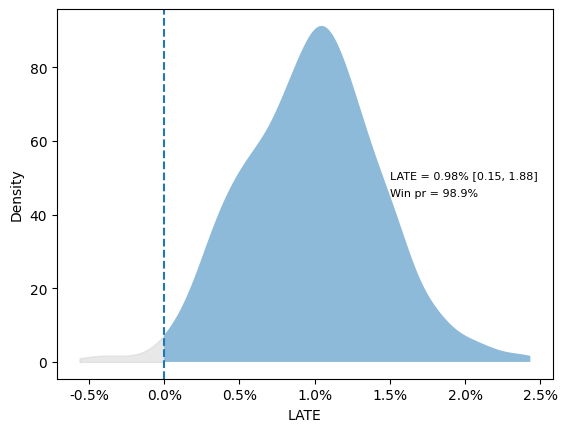
今回の設定では真のLATEは1%としており、求めたLATEの事後分布を見てみるとうまく推定できていることがわかります（事後平均: 約0.98%）。また、LATEが0以上となる確率を求めれば、簡単に勝率を得ることもできます。

おわりに

ランダムな割り当てをしたのにも関わらず、処置群のユーザーが実際には処置を受け取っていなかったという状況は、広告や訴求配信などの効果検証で頻繁に発生すると考えられます。また、検証では新施策の統計的有意性よりも既存ロジックと比べてどの程度有効なのかを直感的・定量的に評価したいという場面もあるでしょう。今回紹介したベイジアン操作変数法は、そうした課題に対処できる非常に優れたアプローチです。

皆様も是非、ベイジアンIVを用いたA/Bテストをお試しください。

よい効果検証を！

References

  • Angrist, J. D., Imbens, G. W., & Rubin, D. B. (1996). "Identification of causal effects using instrumental variables" Journal of the American statistical Association, 91(434), 444-455.
  • Imbens, G. W., & Rubin, D. B. (1997). "Bayesian inference for causal effects in randomized experiments with noncompliance". The annals of statistics, 305-327.
  • Imbens, G. W., & Rubin, D. B. (2015). Causal inference in statistics, social, and biomedical sciences. Cambridge university press.

*1:研究開発部のA/Bテストの取り組みについて、こちらも併せてご覧ください。

*2:実際には Z_iがランダムであること+Stable Unit Treatment Value Assumption（SUTVA）も満たされなければなりません。SUTVAをかみ砕いて言えば①実験対象者間での相互干渉が存在しない②処置の一意性といった仮定であり、因果推論や効果検証では根本的な仮定と言えるでしょう。ちなみに、SUTVAの発音は「ストゥヴァ」「ストゥーヴァ」「スッヴァ」「サトヴァ」など人によりさまざまです。

*3: Z_iがランダムであれば、 ITT = \mathbb{E}[Y_i \mid Z_i = 1] - \mathbb{E}[Y_i \mid Z_i = 0]となります。また、割り当て効果 \mathbb{E}[D_i(1) - D_i(0)]も同様にして \mathbb{E}[D_i \mid Z_i = 1] - \mathbb{E}[D_i \mid Z_i = 0]であり、これは \Pr(\text{compliers and always-taker}) - \Pr(\text{always-taker}) = \Pr(\text{complier})となります。

*4:今回の設定ではアウトカムが二値のものを利用しましたが、アウトカムが連続値でもカウントでも適切な確率分布（連続値であれば正規分布、カウントであればポアソン分布）を利用することでベイジアン操作変数法を応用できます。

© Sansan, Inc.